На координатной прямой расстояние между точками всегда является положительным числом и равняется модулю разности координат конца и начала отрезка, заданного этими точками. Так, расстояние между точками А (а) и B (b) составляет
АВ = |b - а|.
Таким образом, расстояние между заданными по условию точками А и В:
а) при а = 2, b = 8
АВ = |8 - 2| = 6;
б) при а = -3, b = -5
АВ = |-5 - (-3)| = |-2| =2;
в) при а = -1, b = 6
АВ = |6 - (-1)| = 7.
ответ: расстояние между точками А и B равно: а) 6; б) 2; в) 7
Объяснение:
сори если что-то не правильно
170 см²
Объяснение:
У меня немного визуально кривоватый рисунок, но в целом он верен.
Для начала вспомним, как находить площадь параллелограмма. Вот формула для ее нахождения: S=ah (где h-высота; a-сторона, к которой проведена высота).У нас есть прямая AP, которая со стороной MT образует угол PAM, который равен 90°, а следовательно АР является высотой этого параллелограмма.Численно нам известна сторона МТ(МТ=7+10=17см), к которой проведена высота АР, но не известна сама высота. Рассмотрим треугольник АРТ, мы знаем, что угол А равен 90°, угол Р равен 45°, значит угол Т=180-90-45=45°; т.к. углы при основании равны, то треугольник является равнобедренным и его боковые стороны равны, а значит АТ=АР=10 см.Теперь по формуле узнаем площадь: S=17*10=170 см²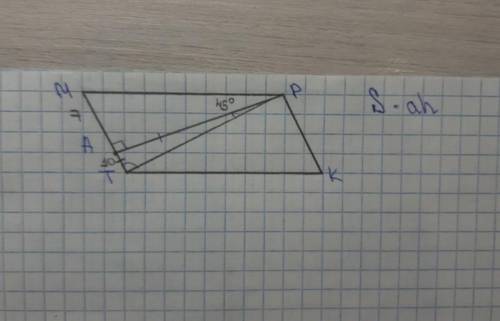
х+х+3=25
2х+3=25
2х=25-3
2х=22
х=11
х+3=14
11+14=25