Биссектриса углов А и Д параллелограмма АВСД пересекаются в точке М, дежащий на стороне ВС. Луч ДМ пересекает прямую АВ в точке N. Найдите периметр параллелограмма АВСД, если АN=10 СМ
РЕШЕНИЕ
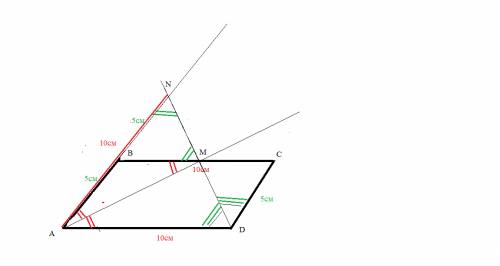
сделаем построение по условию
<ADN=<CDN т.к. DN - биссектриса <D
(AN) || (CD) тогда <AND=<CDN -скрещивающиеся углы
треугольник NAD - равнобедренный (<AND=<АDN )
|AN|=|AD\=10см
(АМ) - биссектриса, высота, медиана
по теореме Фалеса параллельные прямые (AD) || (BC) отсекают на сторонах <AND
пропорциональные отрезки , т.к. | NM |=| MD | следовательно |NB| = |АB| =|AN| / 2=10/2=5см
ПЕРИМЕТР параллелограмма AB+BC+CD+DA=5+10+5+10=30 см
ответ периметр 30см
Объяснение:
1а) в приложенном файле.
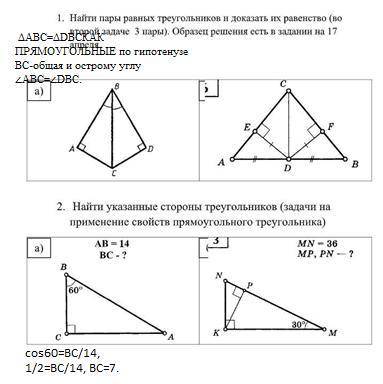
1б)ΔKMN-прямоугольный , по свойству угла 30°⇒ KN=0,5*36=18.
Пусть NP=х , тогда РМ=36-х. Катет в прямоугольном треугольнике есть среднее пропорциональное между проекцией и гипотенузой : KN=NP*NM или 18²=х*36 , х=9, NP=9 , РМ=36-9=27
2б)
1)ΔСЕD=ΔCFD как прямоугольные по катетам ЕD=DF и гипотенузе CD-общая. В равных треугольниках соответственные элементы равны :∠ЕCD=∠FСD и СЕ=СF.
2)∠АЕD=∠ВFD=90.
ΔАЕD=ΔВFD как прямоугольные по катетам ЕD=DF и гипотенузам АD=DВ . В равных треугольниках соответственные элементы равны : АЕ=ВF и ∠А=∠В.
3) Т.к АЕ=ВF и
СЕ=СF , то АС=ВС.
ΔАСD=ΔВСD по стороне и двум прилежащим углам : АС=ВС, ∠ЕCD=∠FСD, ∠А=∠В.
2а) в приложенном файле.
2б)ΔKMN-прямоугольный , по свойству угла 30°⇒ KN=0,5*36=18.
Пусть NP=х , тогда РМ=36-х. Катет в прямоугольном треугольнике есть среднее пропорциональное между проекцией и гипотенузой : KN=NP*NM или 18²=х*36 , х=9, NP=9 , РМ=36-9=27
1/60 часть градуса есть минута.
1/60 минуты - секунда