ответ:4√2 см.
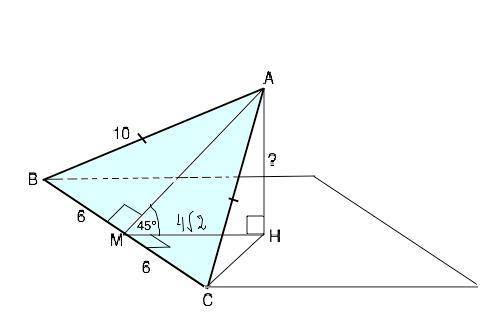
Требуется найти расстояние от вершины А до плоскости, следовательно, основание ВС лежит в проведенной плоскости, с которой плоскость треугольника ВАС образует двугранный угол с ребром ВС. Сделаем и рассмотрим рисунок.
Расстояние от точки до плоскости равно длине опущенного на нее из точки перпендикуляра ⇒ АН - искомое расстояние.
Проведём НМ⊥ВС. По т. о 3-х перпендикулярах наклонная АМ⊥ВС. Отрезки АМ и МН образуют угол 45°. АМ⊥ВС ⇒ АМ является высотой и медианой равнобедренного ∆ ВАС. ∆ ВАМ - египетский, т.к. ВМ:АМ:АВ=3:4:5, ⇒ АМ=8 см ( можно проверить по т.Пифагора). Тогда АН=АМ•sin45°=8•√2/2=4√2 см
Угол А=углу С(углы при основании равнобедренного треугольника)
Угол А=угол ВАD+угол САD
Угол С=угол ВСЕ+угод АВЕ
Так как угол А=углу С, биссектрисы делящиеся их пополам также равны |→ Угог DAC=углу АСЕ Рассмотрим теугольник АМС(М-точка пересечения)
Угол DAC=углу АСЕ(по док 1)
Углы при основании треугольника равны|→ треугольник АМС равнобедренный|→АЕ=ЕD