ответ: V=64√5см³
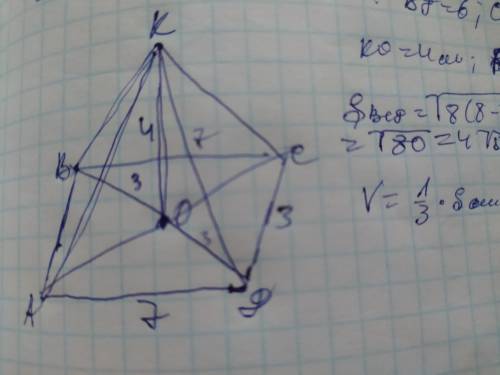
Объяснение: обозначим вершины пирамиды АВСД с высотой КО и диагоналями ВД и АС. Одна диагональ делит параллелограмм на 2 равных треугольника. Пусть ВД=6см. Рассмотрим полученный ∆ВСД. В нём известны 3 стороны и мы можем найти его площадь по формуле: S=√((p-a)(p-b)(p-c)), где а сторона треугольника а р-полупериметр:
Р=3+7+6=16см; р/2=16/2=8см
S=√8((8-7)(8-6)(8-3))=√(8×1×2×5)=
=√80=8√5см²
Так как таких треугольников 2, то площадь параллелограмма=8√5×2=16√5см²
Теперь найдём объем пирамиды зная площадь основания и высоту по формуле: V=⅓×Sосн×КО=
=⅓×16√5×4=64√5/3см³
Ломаная - это фигура, не лежащая на одной прямой.
Звенья - это отрезки, из которых составлена ломаная.
Концы отрезков - вершины ломаной
Длина ломаной - сумма длин всех звеньев.
2. . Многоугольник - это геометрическая фигура, состоящие из замкнутой ломаной.
Сторона - один отрезок многоугольника
Диагональ - отрезок соединяющий две любые не соседние вершины.
Вершина - место пересечений линий в многоугольнике
Периметр - длина ломаной.
3. Выпуклый многоугольник - это мнгоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
4. (n -2) . 1800
n - кол- во углов
5. стр. 99 Так как сумма углов выпуклого n-угольника равна (n-2)*180˚, то сумма углов четырёхугольника равна 360˚
6.
7. Параллелограмм - это четырёхугольник, у которого противолежащие стороны попарно параллельны. Является выпуклым четырехугольником.
8-9
Для параллелограмма верно свойство: Противолежащие стороны попарно равны.
А еще есть признак параллелограма: если в четырехугольнике противолежащие стороны попарно равны, то он паралеллограмм.
10 - 101-102
11. Трапеция - четырёхугольник у которого две стороны параллельны а две другие не параллельны
Стороны - основания и боковые стороны.
12 Трапеция, у которой боковые стороны равны между собой, называется равнобедренной.
Трапеция, один из углов которой прямой, называется прямоугольной.
14 Прямоугольник - это паралелограмм, у которого все углы прямые
Док-во на стр. 108
14 стр. 108
15. Ромб - это паралелограмм, у которого все стороны равны. Док-во - стр. 109.
17.Квадрат - прямоугольник, у которого все стороны равны.
18 Две точки называются симметричными относительно прямой а, если это прямая проходит через середину отрезка и перпендикулярна к нему.
19. . Фигура называется симметричной относительно прямой а, если каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
20. Две точки называются симметричными относительно точки О, если О - середина отрезка.
21.Фигура называется симметричной относительной точки О, если каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Так как периметр ромба равен 16, то сторна ромба равна 16/4=4
Ромб АВСД, пусть угол при В = Х градусов, а при А =2Хградусов (по условию.)Диагонал АС=? Проведем и диагональ ВД. В ромбе диагонали пересекаясь(точка пересечения О), образуют угол в 90 градусов, также диагонали являются биссектрисами.Значит треугольник АОВ прямой.Угол ВАО=2х/2=х, а угол АВС=х/2.
В треугольнике сумма углов равна 180, значит
х+х/2=90
3х/2=90
3х=180
х=180/3
х=60
Угол ВАС=60, тогда угол АВО=60/2=30
В прямоугольном треугольгике, катет лежащий против угла в 30 градусов равен половине гипотенузе, так АВ=4, АО=2, а длина АО=ОС=2 (диагонали ромба в точке пересечения делятся пополам), значит АС=4.
Можно решить еще и так
угол ВАС=углу ВСА=х, также угол В=х, значит треугольник АВС равносторонний и АС=АВ=4
Меншая диагональ ромба равна 4 см.