Основанием конуса будет большее сечение шара, так как радиус основания конуса равен радиусу шара по условию. Значит, высота конуса тоже равна радиусу шара.
Объем конуса находят по формуле:
V = ⅓ * π * R ² * h, где R - радиус основания, h - высота конуса.
Так как высота конуса равна радиусу шара формула примет вид:
V = ⅓ * π * R ³.
Объем шара: V = (4 * π * R ³) / 3. V = 36 ( по условию )
36 * 3 = 4 * π * R ³
108 = 4 * π * R ³
π * R ³ = 27.
Подставим значение π * R ³ в формулу объема конуса:
V = ⅓ * 27 = 9.
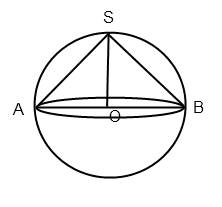
Основанием конуса будет большее сечение шара, так как радиус основания конуса равен радиусу шара по условию. Значит, высота конуса тоже равна радиусу шара.
Объем конуса находят по формуле:
V = ⅓ * π * R ² * h, где R - радиус основания, h - высота конуса.
Так как высота конуса равна радиусу шара формула примет вид:
V = ⅓ * π * R ³.
Объем шара: V = (4 * π * R ³) / 3. V = 36 ( по условию )
36 * 3 = 4 * π * R ³
108 = 4 * π * R ³
π * R ³ = 27.
Подставим значение π * R ³ в формулу объема конуса:
V = ⅓ * 27 = 9.

1) В плоскости СДЕ провести отрезок ЕВ1, равный АВ и параллельный ему. Он одновременно находится в плоскости СДЕ и в вертикальной плоскости МАВ. Поэтому точка F пересечения отрезка МВ с плоскостью СДЕ находится на пересечении отрезков МВ и ЕВ1.
2) В плоскости МАВ 2 подобных треугольника: МЕF и FF1B ( точка F1 - проекция точки F на АВ).
Отрезок FF1 равен ЕА.
Поэтому F1B = (3/2)*10 = 15 см.
АF1 = ЕF = 10 см.
Отсюда АВ = 10+15 = 25 см.
Примечание: данное решение - частный случай, так как где бы ни находилась точка М, ∆ MFE и ∆ AMB остаются подобными, отношение ЕF:AB=2:5, и АВ получается равным 25.