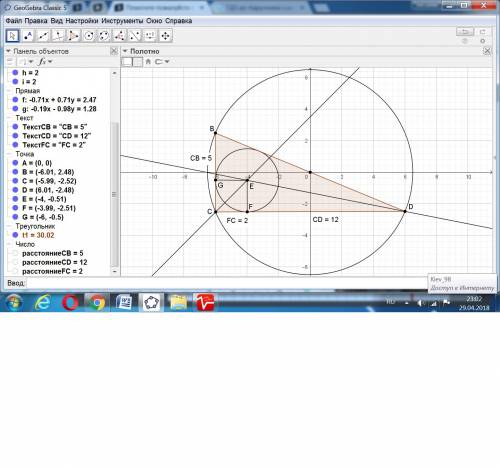
Пусть есть треугольник с катетами AB и BC.
Если радиус описанной окружности равен 6,5, то гипотенуза равна 2*6,5 = 13.
Отрезки катетов до точки касания вписанной окружности равны 2 и -2.
По свойству касательных гипотенуза равна сумме этих отрезков:
AB - 2 + BC - 2 = 13 или AB + BC=17.
За теоремой Пифагора 13² = AB² + BC².
Возведём в квадрат равенство AB + BC = 17:
AB² + 2AB*BC + BC² = 289. Заменим AB² +BC² = 169.
2AB*BC = 289 - 169 = 120, AB*BC = 120/2 = 60.
Из выражения AB+ BC = 17 выразим BC = 17 - AB и подставим в AB*BC = 60.
Получим: AB(17 -AB) = 60 или 17*AB -AB² = 60.
Получили квадратное уравнение AB² - 17AB + 60 = 0.
Квадратное уравнение, решаем относительно AB.
Ищем дискриминант:
D=(-17)^2-4*1*60=289-4*60=289-240=49;
AB1=(√49-(-17))/(2*1)=(7-(-17))/2=(7+17)/2=24/2=12;
AB2=(-√49-(-17))/(2*1)=(-7-(-17))/2=(-7+17)/2=10/2=5.
ответ: катеты равны 5 и 12.
Параллельность прямых.
Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Дано: параллельные прямые a и b, прямая a пересекает плоскость α в точке C.
Доказать, что прямая b также пересекает плоскость α.
Доказательство. Пусть плоскостью β будет плоскость, в которой лежат параллельные прямые a и b. Тогда плоскости α и β пересекутся по прямой, на пример c так как они имеют общую точку C. Эта прямая c лежит в плоскости β и пересекает прямую a в точке C. А если прямая пересекает одну из параллельных пря мых, то она пересечёт и другие прямые, поэтому прямая c пересекает и прямую b в точке E. Так как прямая c принадлежит и плоскости α, и плоскости β . Получается, что плоскостьα и прямая b пересекаются в точке E, то есть они имеют общую точку E. Лемма дока зана.