30 см³.
Объяснение:
Чтобы найти объем прямоугольного параллелепипеда, надо длину умножить на ширину и на высоту.
Пусть a, b, c - измерения прямоугольного параллелепипеда.
Каждая грань параллелепипеда прямоугольник. Периметр прямоугольника определяется по формуле 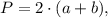 где a и b - стороны прямоугольника.
где a и b - стороны прямоугольника.
Если периметры трех граней по условию равны 10 см,14 см и 16 см, то
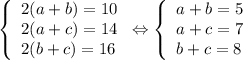
Если сложить все три уравнения системы, то получим
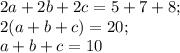
Если  , то
, то 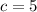
Если 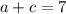 , то
, то 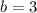
Если  ,то
,то 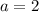
Значит, измерения прямоугольного параллелепипеда
2 см, 3 см и 5 см.
Найдем объем прямоугольного параллелепипеда
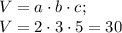
Значит,
объем прямоугольного параллелепипеда равен 30 см³.
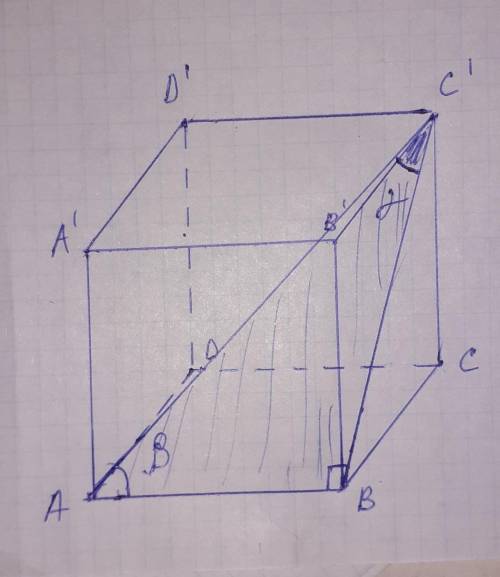
Градусная мера угла между прямыми АС1 и ВС1
<АС1В= arcsin ( 1/√3 ) = 35,2643896828°
Объяснение:
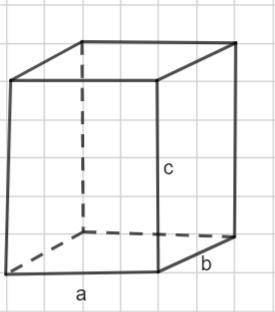
ребро куба а=1
прямая AC1 диагональ куба
прямая ВС1 диагональ грани ВВ1С1С
у куба все 6 граней квадратные
Диагональ квадрата равна d=a√2
ВС1=1√2=√2
прямая АС1 и ВС1 образует с ребром куба АВ прямоугольный треугольник Δ АВС1, где АС1 гипотенуза, ВС1 и АВ соответственно катеты.
находим по теореме Пифагора
АС1=√ВС1²+АВ²=√(√2)²+1²=√2+1=√3
диагональ АС1=√3
АВ противолежит к углу <АС1В , тогда
sin< АС1В=АВ/АС1=1/√3
Градусная мера угла между прямыми АС1 и ВС1
<АС1В= arcsin ( 1/√3 ) = 35,2643896828°