Здесь нужно вспомнить о средней линии треуг-ка. Средняя линия тр-ка - это отрезок, соединяющий середины двух его сторон. Средняя линия параллельна третьей стороне и равна ее половине. MN, NP и РМ - средние линии треуг-ка АВС. Теперь смотрим на наш треуг-к.
В тр-ке MNP и CPN сторона NP общая. NC=1/2BC так как N середина ВС, МР=1/2ВС так как МР - средняя линия. Значит MP=NC. РС=1/2АС так как Р - середина АС, MN=1/2AC так как MN - средняя линия. Значит MN=PC. Получили, что три стороны одного тр-ка соответственно равны трем сторонам другого тр-ка, значит тр-ки равны по 3 признаку.
В параллелограмме противоположные углы равны, противоположные стороны равны и параллельны, а диагонали точкой пересечения делятся пополам.
а)
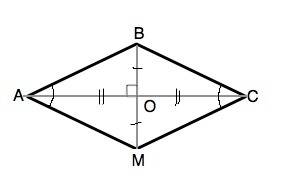
В параллелограмме АВСD диагонали взаимно перпендикулярны. Следовательно, катеты четырех прямоугольных треугольников, образованных диагоналями и сторонами ромба, равны. =>
Эти четыре треугольника равны, значит, их гипотенузы ( стороны параллелограмма) - равны. АВСD- ромб.
б)
Если диагональ параллелограмма - биссектриса его угла, то по свойству равенства накрестлежащих углов при параллельных прямых и секущей она она делит и противоположный угол пополам и является основанием треугольника с равными углами. Равенство углов при основании - признак равнобедренного треугольника.
Поэтому АВ =ВС, ВС =СD, АD =АВ.
Параллелограмм АВСD - ромб.