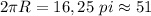периметр P=13+14+15=42
полуперимет p=P/2=21
площадь S=√p(p-a)(p-b)(p-c)=√21(21-13)(21-14)(21-15)=84
радиус описанной окружности R=abc/4S= 13*14*15/4*84=65/8
длина окружности L=2piR=2*3.14*65/8=51.025=51 см
ОТВЕТ 51 см
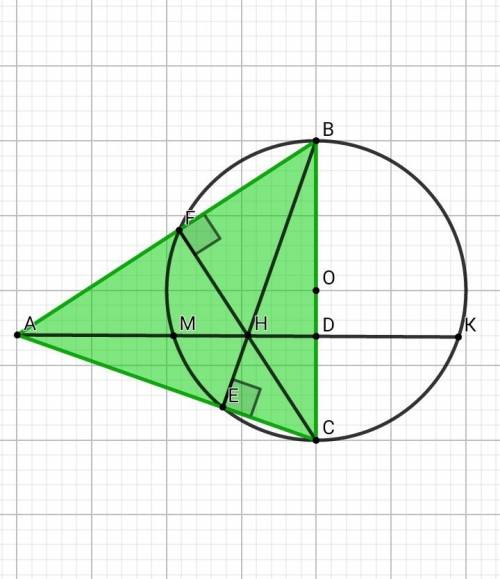
На стороне BC остроугольного треугольника ABC (AB ≠ AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 32, MD = 8, H — точка пересечения высот треугольника ABC. Найдите AH.
Решение.
Проведём построения и введём обозначения как указано на рисунке. Угол — вписанный, опирающийся на диаметр, поэтому он равен 90°. Значит, точка пересечения прямых и — точка пересечения высот Продолжим высоту до пересечения с окружностью в точке Получаем, что По теореме о секущих получаем, что Треугольники и — прямоугольные, угол — общий, следовательно, эти треугольники подобны, откуда:
ответ: 30.
самый простой это решить аналитически выражая площадь через разные формулы:
Формула Герона:
где p - полупериметр
Также площадь треугольника равна:
где R - радиус описанной окружности
Приравняем)
Длина равна