Найдите площадь равнобедренной трапеции описанной, около окружности с радиусом 3, если боковая сторона трапеции делится точкой касания с окружностью в отношении 2:3
Объяснение:( опускаю объяснения как выбиралось отношение 2:3)
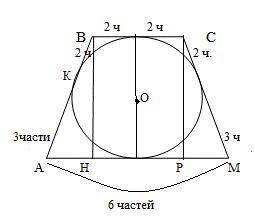
АВСМ-описанная трапеция около окр О(r=3) , АВ=СМ, К- точка касания , ВК:КА=2:3. Найти S.
S=1/2*Р*r , Р=2*АВ+ВС+АМ.
Пусть одна часть х, тогда АК=3х, КВ=2х , АВ=5х.
Т.к трапеция равнобедренная , то АВ=СМ=5х.
По свойству отрезков касательных АМ=3х+3х=6х и
ВС=2х+2х=4х.
Пусть ВН⊥АМ, СР⊥АМ⇒НВСР-прямоугольник и ВС=НР=4х . Значит РМ=АН=(6х-4х):2=1х.
ΔАВН прямоугольный , ВН=3+3=6 , по т.Пифагора АВ²=АН²+ВН²
25х²=х²+36, 24х²=36 , х=√(36/24)=6/(2√6)=√6/2.
Р=2*АВ+ВС+АМ=2*5х+4х+6х=20х , Р=20*(√6/2)=10√6.
S=1/2*10√6*3=15√6 ( ед²)
На шахматном турнире каждый из участников должен был сыграть ровно одну партию с каждым из прочих, но два участника выбыли из турнира, сыграв только по 3 партии. Поэтому число партий, сыгранных в турнире, оказалось равным 110. Сколько всего было участников турнира?
Объяснение:
Пусть первоначально участников было х.
Два участника, которые выбыли , сыграли по 3 партии т.е. :
1 случай ) 3+3=6 , если не играли межлу собой ;
2 случай) 3+2=5 , если одна партия была между выбывшими.
Значит партии, оставшиеся на остальных участников :
1 случай ) 110-6=104 (шт) ;
2 случай ) 110-5=105 (шт).
Оставшиеся участники (х-2) сыграли по одной партии. Таких пар это сочетание из (х-2) по 2 :
С(х-2;2)=104 , С(х-2;2)=104 ,
(х-2)!/(2! * (х -4)!) = 104 ; (х-2)!/(2! * (х -4)!) =105
(х-3) *(х -2)/2 =104 ; (х-3) *(х -2)/2 =105
х²-5х+6=104*2 ; х²-5х+6=105*2
х²-5х-202=0 ; х²-5х-204=0
D=833>0 , D=841>0, х₁=17,
Натуральных корней х₂=-15-не подходит по смыслу задачи.
нет .
Всего участников 17.
2x+2y=360
X=80+y
X+y=180
80+y+y=180
2y=100
Y=50
X=80+50=130
VA=50,vB=130,vC=50,vD=130