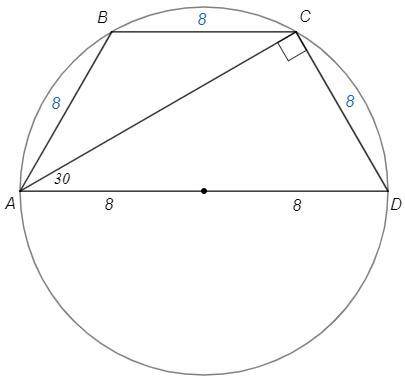
Вписанный прямой угол опирается на диаметр.
ACD=90 => AD=8*2 =16 (диаметр)
Катет против угла 30 равен половине гипотенузы.
CAD=30 => CD=AD/2 =8
Равнобедренная трапеция, боковые стороны равны.
AB=CD =8
Сумма острых углов прямоугольного треугольника 90.
CDA=90-CAD =60
Равнобедренная трапеция, углы при основании равны.
BAD=CDA =60
BAC=BAD-CAD =60-30=30
Вписанный угол равен половине дуги, на которую опирается.
BAC=CAD => ∪BC=∪CD
Равные дуги опираются на равные хорды.
∪BC=∪CD => BC=CD =8
P(ABCD)=8+8+8+16 =40 (см)
Площадь основания равна произведения квадрата стороны на синус угла между сторонами ромба
площадь ромба равна a^2*sin 60=a^2*корень(3)\2
Высота ромба равна площадь ромба\сторону
высота ромба равна a^2*корень(3)\2:а=a*корень(3)\2
Пусть AK - высота ромба
Пусть AK1- высота AD1C1
Тогда KK1 - высота параллелепипеда и угол KAK1=60 градусов
KK1\AK= tg KAK1=корень(3)
высота параллелепипеда равна KK1=AK*корень(3)=
a*корень(3)\2*корень(3)=а*3\2
Площадь боковой поверхности 4*AB*KK1=
4*a*а*3\2=6a^2
площадь поверхности =2* площадь основания + площадь боковой поверхности
2*a^2*корень(3)\2+6a^2=(корень(3)+6)* a^2
ответ: a*корень(3)\2
а*3\2
6a^2
a^2*(корень(3)+6)
решение представлено на фото
Объяснение: