15. треугольник АВС, МН-средняя линия , площадь АМН=21, треугольник АНС , НМ-медиана (АМ=МС), медиана делит треугольник на 2 равновеликих треугольника, площадь АМН=площадь МНС=21, площадь АНС=площадьАМН+площадьМНС=21+21=42, треугольник АВС, АН-медиана (ВН=НС), тогда плошщадь АВН=площадьАНС=42, площадьАВС=площадь АВН+площадьАНС=42+42=84
16. площади подобных многоугольников относятся как периметры в квадрате, 16/49=периметр1 в квадрате/1225, периметр1 в квадрате=16*1225/49=400, периметр1=20
17. треугольник АРД подобен треугольнику ВРС по двум равным углам, уголР-общий, уголА=уголРВС как соответственные, площади подобных треугольников относятся как отношение квадратов подобных сторон, площадь ВРС/площадьАРД=ВС в квадрат/АД в квадрате, площадьВРС/80=9/16, площадьВРС=80*9/16=45, площадьАВСД=площадьАРД-площадьВРС=80-45=35
18, треугольник АВС, АВ=Вс=20, АС=32, проводим высоту ВН=медиане, АН=НС=1/2АС=32/2=16, треугольник АВН прямоугольній, ВН=корень(Ав в квадрате-АН в квадрате)=корень(400-256)=12, tgA=ВН/АН=12/16=3/4=0,75
19. треугольник АВС, уголС=90, ВС=2, АС=4,, АВ=корень(АС в квадрате+ВС в квадрате)=корень(16+4)=2*корень5, cosB=ВС/АВ=2/(2*корень5)=корень5/5
(см. объяснение)
Объяснение:
Приведу 2 решения. Алгебраическое и логическое. Выбирай то, которое тебе проще.
Алгебраический метод:
Достоинства: универсален. Можно решить любую задачу этого рода.
Недостатки: присутствуют вычисления. Есть возможность ошибиться в расчетах. Длительность решения, вызванная расчетами.
Подставляй вместо x число, в каждое уравнение и считай y. Смотри, на каком графике есть полученная координата.
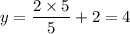
Точка (5; 4) есть только на графике А.
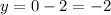
Точка (0; -2) есть только на графике Б.
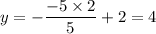
Точка (-5; 4) есть только на графике В.
Тогда получили ответ: А-1, Б-2, В-3.
Решение, основанное на логических рассуждениях:
Достоинства: нет расчетов. Шанс ошибиться стремится к 0. Скорость решения. Используя этот метод можно моментально решать подобные задачи.
Недостатки: требуется соответствующее мышление. Хорошее понимание темы. Знание того, за что отвечает каждый коэффициент в уравнении каждого графика функции.
Рассмотрим графики А, Б и В. Заметим, что график В принципиально отличается от графиков А и Б наклоном прямой. За наклон отвечает число перед x. В вариантах ответа 1 и 2 такие числа одинаковые: 2/5. Значит сразу понятно соответствие B-3. Рассмотрим графики А и Б. Они отличаются тем, что один из них выше другого. За это отвечает число b, (если y=kx+b). Т.е. мы смотрим на число без буквы x. Там, где оно со знаком +, это график А, где со знаком -, то это график Б.
9,2-2,4=6,8
ответ:БС=6,8