Предположим, что прямая а не пересекает плоскости α и β.
Значит, прямая а параллельна обеим плоскостям.
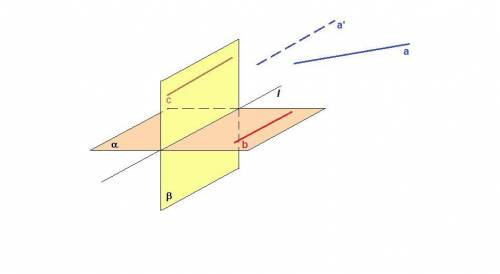
Тогда в каждой плоскости найдется прямая, параллельная прямой а. Пусть это прямые b и с.
Так как b║a и с║а, то b║c.
Если прямая с параллельна прямой b, лежащей в плоскости α, то с║α.
Плоскость β проходит через прямую с, параллельную плоскости α, и пересекает плоскость α, значит линия пересечения плоскостей параллельна прямой с.
Итак, c║l, c║a, ⇒ l║a. Но прямые l и а скрещивающиеся. Получили противоречие.
Значит, прямая а пересекает хотя бы одну из плоскостей.
Пусть А - начало координат.
Ось X - AB
Ось Y -:AC
Ось Z - AD
Координаты точек
В(12;0;0)
С(0;18;0)
D(0;0;5)
M ( 6;9;0)
Вектор DM (6;9;-5)
Его длина
| DM | = √(6^2+9^2+(-5)^2) = √142
Точка пересечения медиан
О делит их в отношении 2:1
О(4;6;0)
Вектора
АО(4;6;0) длина √(4^2+6^2)=2√13
BO(-8;6;0) длина √(8^2+6^2)=10
СО(4;-12;0) длина √(4^2+12^2)=4√10
DO(4;6;-5) длина √(4^2+6^2+5^2)= √77