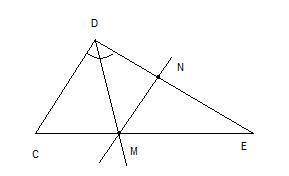
1. После построения MN получается треугольник MNE, подобный треугольнику CDE по первому признаку подобия (угол Е - общий, углы С и NME равны как соответственные углы при пересечении двух параллельных прямых CD и MN секущей СЕ). Поскольку треугольники подобны, то <MNE = <CDE = 68°2. Зная, что развернутый угол равен 180°, находим угол DNM:<DNM = 180 - <MNE = 180 - 68 = 112°3. Поскольку DM - биссектриса, то угол MDN = <CDE : 2 = 68 : 2 = 34°4. Зная два угла треугольника DMN, находим неизвестный угол:<DMN = 180 - <MDN - <DNM = 180 - 34 - 112 = 34°
В правильной треугольной пирамиде полная поверхность равна 16корень из 3 см^2, а площадь основания- 4корень из 3 см^2.Найдите апофему и плоский угол при вершине пирамиды.
Зная площадь основания, найдём величину стороны а основания из формулы So = a²√3/4.
Отсюда a = √(4S/√3) = √(4*4√3/√3) = 4см.
Находим площадь боковой поверхности.
Sбок = S - So = 16√3 - 4√3 = 8√3 см².
Площадь одной боковой грани в 3 раза меньше, поэтому:
Sгр = 8√3/3 см².
Из формулы площади грани как треугольника найдём значение апофемы (это высота боковой грани).
Sгр = (1/2)aA, отсюда находим апофему.
А = 2Sгр/а = 2*(8√3/3)/4 = (4√3/3) см.
Угол при вершине равен 2arctg((a/2)/A) = 2arctg(2/(4√3/3)) =
= 2arctg(3/(2√3) ≈ 81,7868 градуса.
В прямоугольном треугольнике, образованном этой высотой, заданным отрезком и боковой стороной (которая играет роль гипотенузы) катеты равны 8 и 15, соответственно, гипотенуза равна 17. (Это Пифагоров треугольник 8,15,17)
Поэтому площадь треугольника равна 15*17/2 = 127,5
С основанием чуток сложнее, поскольку треугольник с катетами 15 и 17 - 8 = 9 - не Пифагоров, его гипотенуза равна корень(9^2 + 15^2) = 3*корень(34), откуда периметр равен 17*2 + 3*корень(34) = 34 + 3*корень(34);