Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой. Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.
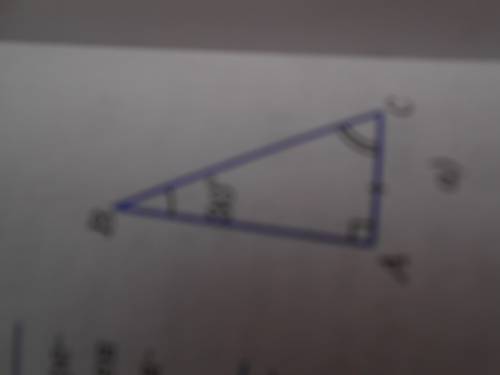
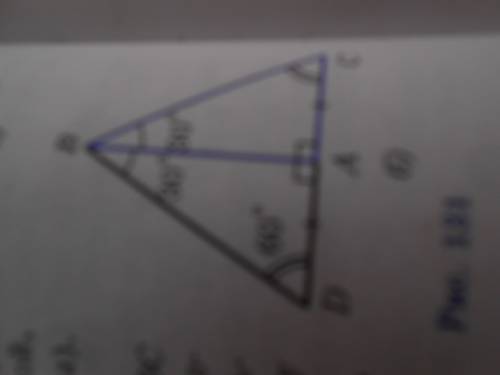
Рассмотрим прямоугольный треугольник АВС, в котором угол А-прямой, угол В=30 градусов и значит угол С=60градусов, Докажем что ас = 1/2ВС
Приложим к треугольнику АВС равный ему треугольник АВД. Получим треугольник ВСД в котором угол В=углу Д=60градусов поэтому ДС=ВС но АС=1/2ДС следовательно АС1/2ВС что и ьребовалось доказать.
Если катет прямоугольного треугольника равен половине гипотенузе, то угол лежащий против этого угла равен 30 градусов.
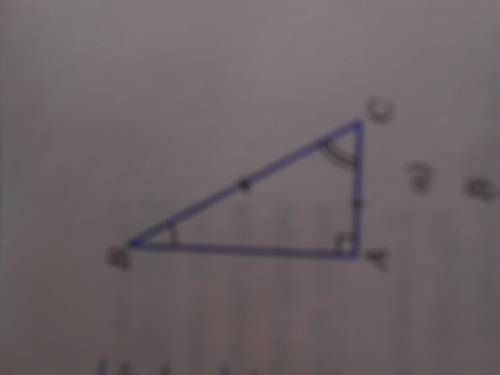
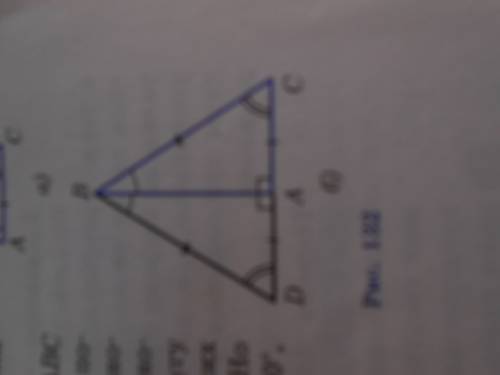
Рассмотрим прямоугольный треугольник авс у которого катет АС равен половине гипотенузы ВС.
Приложим к треугольнику АВС равный ему треугольник АВД. Получим равносторонний треугольник ВСД. Углы равностороннего треугольника равны друг другу, поэтому каждый из углов равен 60 градусов. в ЧАСТНОСТИ угол ДВС =60 градусов. Но угол ДВС =2угла АВС . Следовательно угол авс равен 30 градусов
первые два вложение к первой теореме вторые ко второй теореме
А1. ответ: 4.
А2. ответ: 4.
А3. ответ: 3.
А4. ответ: 1.
В1. Дано: ΔАВС, АВ = ВС = АС + 5 см, Р = 34 см.
Найти: АВ.
Решение: Пусть АС = х см, тогда АВ = ВС = х + 5,
x + (x + 5) + (x + 5) = 34
3x + 10 = 34
3x = 24
x = 8
АС = 8 см
АВ = ВС = 8 + 5 = 13 см
ответ: боковая сторона 13 см.
В2. Дано: ΔАВС, АВ = АС, АМ - медиана, Pabc = 40 см, Pabm = 33 см.
Найти: АМ.
Pabm = 33 см
АВ + ВМ + АМ = 33
2 · (АВ + ВМ + АМ) = 66
Так как АВ = АС, а ВМ = СМ, то
2АВ + 2ВМ + 2АМ = 66
АВ + АС + ВС + 2АМ = 66
2АМ = 66 - (АВ + АС + ВС) = 66 - Pabc = 66 - 40 = 16
AM = 16/2= 8 см
С1. 1) Если сумма равных сторон равна 26 см, то боковые стороны равны по 13 см, а основание - 10 см.
2) Обозначим боковые стороны а и b, основание - с.
а + с = 26 см
Рabc = 2а + с = 36 см
с = 36 - 2а
с = 26 - а
26 - a = 36 - 2a
a = 10 см
c = 16 см
ответ: 13 см, 13 см, 10 см или 10 см, 10 см, 16 см.
7х=14
х=2 см - основание;
2*3=6 см - боковые стороны.
Стороны треугольника - 2 см, 6 см, 6 см.
(сумма любых двух сторон треугольника больше длины третьей стороны).