Объяснение:
В параллелограмме противолежащие стороны равны и противолежащие углы равны.
Доказательство:
Противолежащие стороны параллелограмма параллельны.
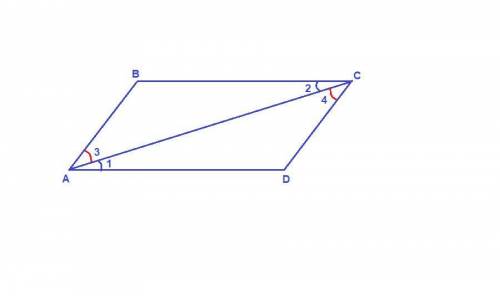
∠1 = ∠2 как накрест лежащие при пересечении параллельных прямых ВС и AD секущей АС,
∠3 = ∠4 как накрест лежащие при пересечении параллельных прямых АВ и СD секущей АС,
АС - общая сторона для треугольников АВС и CDA,
значит ΔАВС = ΔCDA по стороне и двум прилежащим к ней углам.
Тогда ∠В = ∠D, AB = CD и BC = AD.
∠BAD = ∠1 + ∠3
∠BCD = ∠2 + ∠4,
∠1 = ∠2 и ∠3 = ∠4, ⇒ ∠BAD = ∠BCD
4√2 см
Объяснение:
Имеем прямоугольный треугольник АОВ, где АВ=8 см, ∠В=45°. Найти ОВ.
Если ∠В=45°, то и ∠А=45°, т.к. сумма острых углов прямоугольного треугольника составляет 90°.
Значит, ΔАОВ - равнобедренный, АО=ВО.
Пусть АО=ВО=х см, тогда по теореме Пифагора
АВ²=х²+х²
АВ²=2х²
64=2х²
х²=32
х=√32=4√2
ОВ=4√2 см