меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
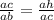
теперь подставим наши значения в эту пропорцию:
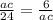
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см
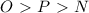- всё это конечно углы.
Якщо довжини всіх сторін паралелограма однакові (a), то цю фігуру можна назвати ще й квадратом. Величини всіх його кутів дорівнюють 90 °, а довжини діагоналей (L) однакові і можуть бути розраховані по теоремі Піфагора для прямокутного трикутника. Помножте довжину сторони квадрата на корінь з двійки - результат і буде довжиною кожної з його діагоналей: L = a *? 2.
2Якщо про параллелограмме відомо, що він є прямокутником із зазначеними в умовах довжиною (a) і шириною (b), то і в цьому випадку довжини діагоналей (L) будуть рівні. І тут теж задійте теорему Піфагора для трикутника, в якому гіпотенузою є діагональ, а катетами - дві суміжні сторони чотирикутника.
3Шукану величину розрахуйте витяганням кореня з суми зведених в квадрат ширини і висоти прямокутника: L =? (A? + B?).
Для всіх інших випадків знання одних тільки довжин сторін вистачить лише для визначення величини, що включає в себе довжини відразу обох діагоналей - сума їх квадратів за визначенням дорівнює подвоєною сумі квадратів довжин сторін. Якщо ж на додаток до довжин двох суміжних сторін паралелограма (a і b) відомий ще і кут між ними (?), То це дозволить розрахувати довжини кожного відрізка, що з'єднує протилежні кути фігури. Довжину діагоналі (L?), Що лежить навпроти відомого кута, знайдіть по теоремі косинусів - складіть квадрати довжин суміжних сторін, від результату відніміть твір цих же довжин на косинус кута між ними, а з отриманої величини витягніть квадратний корінь: L? =? (A? + B? -2 * A * b * cos (?). Для знаходження довжини іншої діагоналі (L?) Можна скористатися властивістю паралелограма, наведеним на початку цього кроку - подвійте суму квадратів довжин двох сторін, від результату відніміть квадрат вже розрахованої діагоналі, а з отриманого значення витягніть корінь. У загальному вигляді цю формулу можна записати так: L? =? (A? + B? - L??) =? (A? + B? - (A? + B? -2 * A * b * cos (?) =? (A? + B? - a?-b? +2 * a * b * cos (?) =? (2 * a * b * cos (?).