П равильная четырехугольная призма - это многогранник, основания которого являются правильными четырехугольниками - квадратами, а боковые грани — равными прямоугольниками.
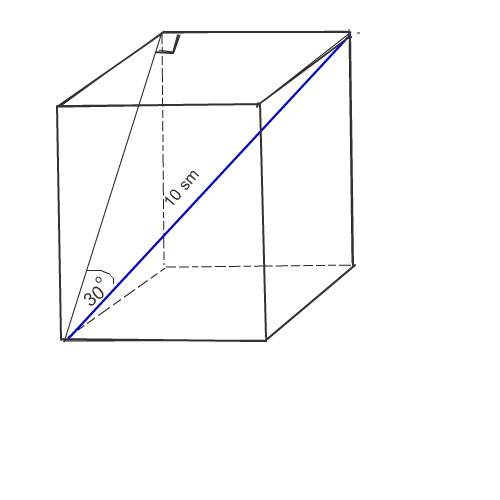
Так как сторона квадрата ( верхнего основания призмы) противолежит углу 30 градусов, она равна половине диагонали призмы и равна 5 см.
Нужно теперь найти высоту призмы.
Для этого придется найти диагональ боковой грани из треугольника, гипотенузой в котором является диагональ призмы, а катетами сторона квадрата и диагональ боковой грани.
Она равна
√(100 -25)= √75 =5√3
Теперь находим высоту призмы
h² =(5√3)² -5² =√50=5√2
Площадь полной поверхности призмы равна площади ее четырех боковых граней плюс площадь оснований.
Площадь боковых граней равна
4*5*5√2=100√2
Площадь оснований
2*5*5=50 см²
Площадь полной поверхности призмы
100√2 +50=50(2√2+1) см
27 дм - длина меньшего катета прямоугольного треугольника.
Объяснение:
Так как треугольник прямоугольный, то центр окружности лежит на середине гипотенузы. То есть диаметром описанной окружности будет гипотенуза треугольника. Значит гипотенуза равна 22,5*2=45 дм. Получается прямоугольный треугольник с катетом 27 дм и гипотенузой 45 дм. Пусть х дм - длина другого катета. По теореме Пифагора:
27²+х²=45²
х²=45²-27²
х²=2025-729
х²=1296
х=36 дм - длина второго катета.
Отрицательный корень в этом уравении лишен смысла.
Меньшим из этих катетов будет катет длиной 27 дм.
Значит в ответе катет длиною 27 дм.
2) 180 град
3) 120 град
4) 30 град
5) 150 град