ответ: боковая поверхность заданной пирамиды равна 120 см².
Решение.
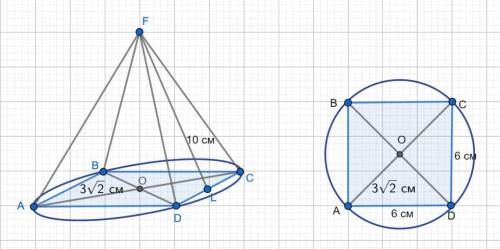
Дана правильная четырехугольная пирамида. в основании ее лежит квадрат. Точка пересечения диагоналей квадрата является центром описанной около квадрата окружности, а радиус ее равен половине диагонали квадрата.
Так как радиус описанной окружности AO = 3√2, то диагональ квадрата AC = 2*3√2 = 6√2.
Найдем сторону квадрата ABCD по т.Пифагора:
AC² = AD² + CD² = 2AD²; (6√2)² = 2AD²; 36*2 = 2AD²; AD² = 36; AD = 6 см.
Сторона квадрата = 6 см. Периметр основания пирамиды P = 4AD = 4*6 = 24 см.
Боковая поверхность пирамиды равна половине произведения периметра основания на апофему.
Sбок = (1/2) * P * h = 1/2 * 24 * 10 = 120 (см²).
Так как АМ=МБ, АД=ВС и МС=МД, то треугольники АМД и ВБС по 3 признаку равенста трегольников(по 3 сторонам). Так как эти треугольники равны, значит и углы у них равны( уголВСМ=углуМДА, уголСВМ=углу МАД, угол СМВ=углу ДМА). Угол ДАМ и СВМ односторонние, значит их сумма должна быть 180(так как ВС параллелен АД, а АВ их пересекает), а при пересечении 2 параллелей сумма односторонних углов равна180, из этого следует угол ДАМ и СВМ равны 90 градусов, а если в параллелограмме хотя бы один угол прямой, то это прямоугольник.Вот.