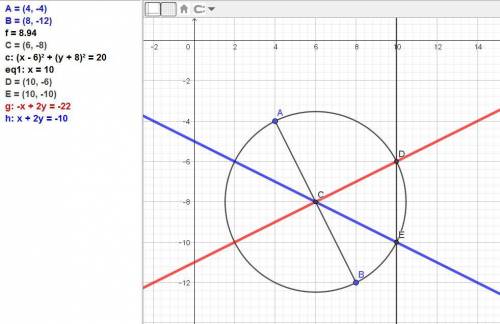
Даны точки А(4;-4) и В(8;-12) как концы диаметра окружности.
Находим её центр О.
Координаты точки О = (А(4;-4) + В(8;-12))/2 = (6; -8).
Радиус R = √((6-4)² + (-8-(-4))²) = √(4 + 16) = √20 = 2√5.
Определяем уравнение этой окружности.
(x - 6)² + (y + 8)² = 20.
Теперь можно определить координату по оси Оу точки К, зная, что х = 10. Подставим х = 10 в уравнение окружности.
(10 - 6)² + (y + 8)² = 20,
16 + (y + 8)² = 20,
(y + 8)² = 4, извлечём корень из обеих частей.
у + 8 = +-2. Получаем 2 значения: у1 = -8 + 2 = -6, у2 = - 8 - 2 = -10.
Заданных прямых тоже две: ОД и ОЕ.
Векторы: ОД = (4; 2), ОЕ = (4; -2).
Уравнение ОД: (х - 6(/4 = (у + 8)/2 или в общем виде х - 2у - 22 = 0.
Уравнение ОЕ: (х - 6(/4 = (у + 8)/(-2) или в общем виде х + 2у + 10 = 0.
В правильной четырёхугольной пирамиде сторона основания равна 10 м, а высота - 12 м. Найдите площадь поверхности пирамиды.
===========================================================
В правильной четырёхугольной пирамиды основанием является квадрат, вершина проецируется в центр основания, то есть точку пересечения диагоналей квадрата и боковые грани представляют собой равные треугольники.Из т. О - точки пересечения диагоналей опустим на CD перпендикуляр ОН МО⊥(ABC) , OH∈(ABC) , OH⊥CD ⇒ по теореме о трёх перпендикулярах МН⊥CDOH⊥CD , AD⊥CD , AO = OC ⇒ СН = НD ⇒ OH - средняя линия ΔACD ⇒ OH = AD/2 = 10/2 = 5 мВ Δ МОН: по т. Пифагора МН² = МО² + ОН² = 12² + 5² = 144 + 25 = 169 ⇒ МН = 13 мПлощадь полной поверхности пирамиды равна:S = S бок. + S осн. = 4•S bcd + S abcd = 4•(1/2)•10•13 + 10² = 260 + 100 = 360 м²ОТВЕТ: 360 м²