Объяснение:
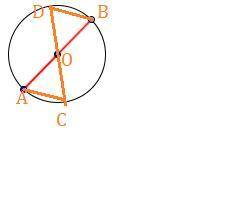
1)Дано окр. О(r) , АВ, СD-диаметры .
Доказать АС=BD
Доказательство.ΔАОС=ΔВОD по двум сторонам и углу между ними : АО=ОВ и СО=ОD как радиусы одной окружности, ∠АОС=∠ВОD как вертикальные .
2) Дано окр. О(r) , r=9 см , АВ, АС-касательные, ∠ВАС=120°.
Найти: АВ , АС.
Решение. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания ⇒∠ОВА=∠ОСА=90°. Проведем АО.
Отрезки касательных к окружности, проведенных из одной точки, равны , т.е АВ=АС , и составляют равные углы с прямой, проходящей через эту точку и центр окружности, т.е. ∠ВАО=∠САО=120°:2=60°.
ΔВАО : ∠ВОА=90°-60°=30°. Пусть АВ=х , по св. угла 30° ⇒ОА=2х. По т. Пифагора (2х)²=х²+9² или 3х²=81 или х²=27 или х=3√3. АВ=АС=3√3 см

Объяснение:
1)Дано окр. О(r) , АВ, СD-диаметры .
Доказать АС=BD
Доказательство.ΔАОС=ΔВОD по двум сторонам и углу между ними : АО=ОВ и СО=ОD как радиусы одной окружности, ∠АОС=∠ВОD как вертикальные .
2) Дано окр. О(r) , r=9 см , АВ, АС-касательные, ∠ВАС=120°.
Найти: АВ , АС.
Решение. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания ⇒∠ОВА=∠ОСА=90°. Проведем АО.
Отрезки касательных к окружности, проведенных из одной точки, равны , т.е АВ=АС , и составляют равные углы с прямой, проходящей через эту точку и центр окружности, т.е. ∠ВАО=∠САО=120°:2=60°.
ΔВАО : ∠ВОА=90°-60°=30°. Пусть АВ=х , по св. угла 30° ⇒ОА=2х. По т. Пифагора (2х)²=х²+9² или 3х²=81 или х²=27 или х=3√3. АВ=АС=3√3 см


7
Объяснение:
Пусть AD = 9x, a CD = 40x. Тогда высота в квадрате => 80 = 9x*40x => x^2 = 80/360 => x = √2/3
AD = 9*√2/3 = 3√2
CD = 40*√2/3 = 40√2/3
Найдем площадь треугольника ABC потом разделим ее на два получим площадь одной части, а так как прямая а образует подобный треугольник с треугольником BDC найдем его площадь и коэф. подобия ну и найдем а.
S = 49√2/3 * 4√5 * 1/2 = 98√10/3 S/2 = 49√10/3
Sbdc = 40√2/3*4√5 * 1/2 = 80√10/3
коэф. подобия в квадрате k^2 = (80√10/3):49√10/3 = 80/49; k = 4√5/7
a = 4√5 : 4√5/7 = 7