а) Треугольник АВС равнобедренный с боковыми сторонами АВ=ВС. б) В треугольнике АВС: ∠А = ∠С = 70°, ∠В = 40°.
Объяснение:
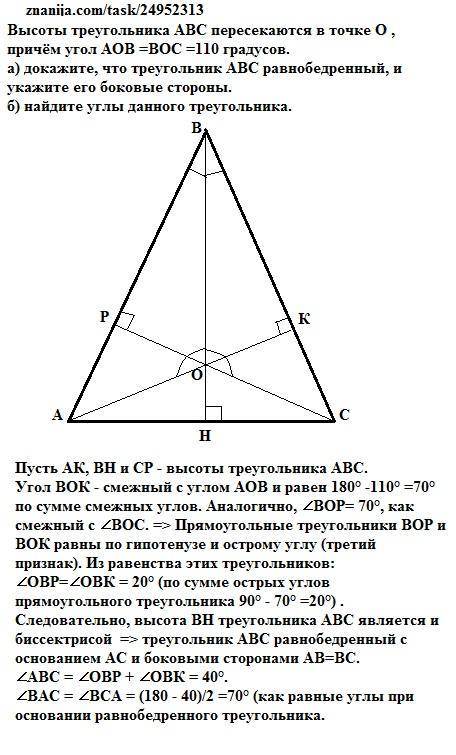
Пусть АК, ВН и СР - высоты треугольника АВС.
Угол ВОК - смежный с углом АОВ и равен 180° -110° =70°по сумме смежных углов. Аналогично, ∠ВОР= 70°, как смежный с ∠ВОС. => Прямоугольные треугольники ВОP и ВОК равны по гипотенузе и острому углу (третий признак). Из равенства этих треугольников:
∠ОВР=∠ОВК = 20° (по сумме острых углов прямоугольного треугольника 90° - 70° =20°) .
Следовательно, высота ВН треугольника АВС является и биссектрисой => треугольник АВС равнобедренный с основанием АС и боковыми сторонами АВ=ВС. Что и требовалось доказать.
∠АВС = ∠ОВР + ∠ОВК = 40°.
∠ВАС = ∠ВСА = (180 - 40)/2 =70° (как равные углы при основании равнобедренного треугольника.
x₀ = (x₁ + х₂)/2 = (4 + 0)/2 = 2
y₀ = (y₁ + y₂)/2 = (3 + 3)/2 = 3
O( 2 ; 3 )
Найдем длину диаметра AB:
AB = √((x₁ - х₂)² + (y₁ + y₂)²) = √((4 - 0)² + (3 - 3)²) = √(16 + 0) = 4
Значит радиус R = 2.
Уравнение окружности:
(x - x₀)² + (y - y₀)² = R²
(x - 2)² + (y - 3)² = 4