1)
полная окружность 360 град ; 9/11 - всего 20 частей
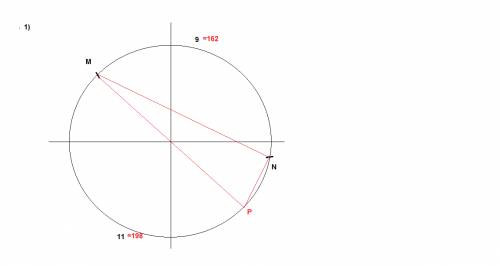
дуга (9) = 9/20*360=162 град
дуга (11) =11/20*360=198 град
вершина N- лежит на окружности
сторона MP- совпадает с диагональю
свойство прямоугольного треугольника , вписанного в окружность
треугольник МNP - прямоугольный
<MNP=90 град
<MPN (вписанный)-опирается на дугу MN=162 град
свойство вписанного угла (он равен половине дуги, на которую опирается)
<MPN=1/2*162=81 град
<NMP=90- <NPM=90-81=9 град
ответ углы 90 ;81;9 град
1) апофема равна 3
2) площадь нижнего основания равно 81см²
3) площадь верхнего основания равно 1см²
4) площадь боковой поверхности 60см²
5) площадь полной поверхности 142см²
Объяснение:
MP=A'D'=1см
AM=(AD-MP)/2=(9-1)/2=8/2=4см
Теорема Пифагора
А'М=√(АА'²-АМ²)=√(5²-4²)=3см. апофема
Sбок=4*АМ(А'D'+AD)/2=4*3(1+9)/2=
=12*10/2=60см²
Sосн'=А'В'²=1²=1см²
Sосн=АВ²=9²=81см²
Sпол=Sосн'+Sосн+Sбок=60+81+1=142см²
Хотелось найти апофему через высоту пирамиды.
АС=АВ√2=9√2см
А'С'=А'В'√2=1√2см.
НК=А'С'=√2см.
АН=(АС-НК)/2=√(9√2-√2)/2=4√2
∆АА'Н- прямоугольный треугольник
Теорема Пифагора
А'Н=√(АА'²-АН²)=√(5²-(4√2)²)=√(25-32)
Условие не корректно.
Нет высоты, нет апофемы, нет площади боковой поверхности, нет площади полной поверхности.