1)а
2)по углам:а по сторонам:б
3)AB=AC+BC=8,5см
4)в (сумма острых углов в прямоугольном треугольнике равна 90°)
5)6+6+9=21см
6)б
2 часть
1)в равнобедренном треугольнике углы при основании равны, следовательно они равны 130°/2=65°
Сумма углов в треугольнике равна 180°. 180°-(65°+65°)=50°
ответ:65°,65°,50°
2) периметр ABD равен 17см, а высота равна 6, следовательно AB+AD=17-6=11 см. BD - медиана, следовательно AD=BD.
Рассмотрим треугольники ABD и CBD:
1)BD - общая сторона
2)AD=BD
3)ADB=CDB
Следовательно треугольники равны по двум сторонам и углу между ними.
Следовательно периметр треугольника АВС равен 11+11=22 см.
ответ: 22см.
Объяснение:
1.Продолжите предложение. А) Центральный угол-это угол , вершина ,которого в центре окружности , а стороны пересекают окружность
Б) Угол между касательной и хордой равен равен половине дуги, которую стягивает данная хорда.
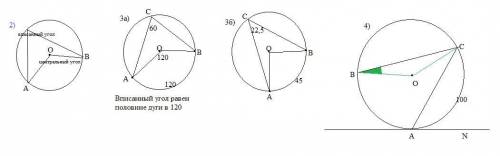
2.Постройте окружность, обозначьте её центр точкой О и постройте вписанный центральный углы, опирающиеся на дугу АВ. (в приложении)
3.А) Постройте центральный угол 120 градусов и дополните рисунок вписанным углом, опирающимся на эту дугу и найдите градусную меру вписанного угла. ( в приложении)
Б) Постройте острый вписанный в окружность угол и найдите градусную меру центрального угла, опирающегося на эту дугу. ( в приложении)
4.Дана окружность с центром в точке О, АN-касательная, СВ и СА- хорды. Известно, что дуга АС равна 100 градусам, дуга АВ относится к дуге ВС как 2 к3. Дуги АВ и ВС меньше полуокружности.
Найдите: а) углы САN, АОВ, АСВ, СВО; б)дуги АВ и СВ.
Решение.
а)∠САN=1/2*100°=50° по правилу п.1Б;
б)Пусть одна часть дуги х°, тогда из условия ∪АВ:∪ВС=2:3 ,
получаем :∪АВ=2х ,∪ВС=3х.
Вся окружность 360°⇒2х+3х+100=360 или 5х=260 или х=52°.
Значит ∪АВ=104° ,∪ВС=156°.
а)∠АОВ=∪АВ , как центральный⇒ ∠АОВ=104°,
∠АСВ=1/2*∪АВ , как вписанный ⇒∠АСВ=52°,
∠СВО=?. Рассмотрим ΔСВО-равнобедренный, т.к. ОВ=ОС как радиусы.∠ВОС=∪ВС=156°. Значит ∠ВСО=∠СВО=(180°-156°):2=12°
Левая часть средней линии равна половине верхнего основания, а правая часть - половине нижнего основания.
Отсюда ответ:
средняя линия трапеции делится пополам точкой пересечения с одной из диагоналей когда верхнее и нижнее основания равны, то есть когда трапеция становится прямоугольником.