а) Координаты середины отрезка равны полусуммам соответствующих координат его концов.
А (2; -1; 0), В (-4; 2; 2)
Обозначим середину отрезка АВ буковой К
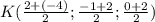
К (-1; 0,5; 1)
б) Нужно найти координаты точки С, если точка В является серединой отрезка АС. Координаты точек А и В известны. Координаты точки С обозначим (x; y; z). И используем формулу для нахождения координат середины отрезка. Находим координаты середины отрезка АС.
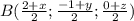
Координаты точки В известны. Приравняем их и получим три уравнения, решая которые найдем координаты точки С.
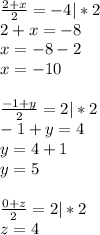
C (-10; 5; 4)
в) Длина отрезка можно вычислить так: квадратный корень из суммы квадратов разностей соответствующих координат концов отрезка.
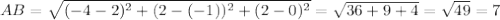
АВ=7
По сумме углов треугольника ∠BAD=180-(40+40)=180-80=100°
∠BAD=∠BCD=100°
По сумме углов четырехугольника ∠ABC+∠ADC=360-(100+100)=360-200=160°
∠ABC=∠ADC (из свойств параллелограмма)
∠ABC+∠ADC=2∠ABC=160°
∠ABC=80°=∠ADC
ответ: 100°,80°