Найди площадь круга, вписанного в равнобедренную трапецию с основаниями длиной 6 см и 12 см и периметром 36 см
Объяснение:
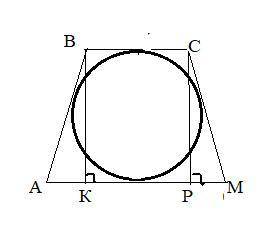
АВСМ- описанная трапеция⇒ суммы длин противоположных сторон равны. Т.е 6+12=АВ+СМ⇒ АВ=СМ=9 см. Пусть ВК⊥АМ , СР⊥АМ.
S(круга)=πr². Радиус вписанной в трапецию окружности будет равен половине высоты трапеции.
Т.к. ВК⊥АМ , СР⊥АМ, то КВСР-прямоугольник ⇒
КР=6 см, АК=РМ=(12-6) :2=3 (см).
ΔАВК-прямоугольный, по т. Пифагора ВК=√(9²-3²)=√18=3√2(см).
ВК-высота трапеции, значит r=(3√2)/2 см.
S(круга)= π ( (3√2)/2 )²=4,5π (см²)
Объяснение:
1. а) BT биссектриса, б) ВД высота, в) ВЕ медиана, г) MN средняя линия
2. ∠AKE=∠CKE ( так как КЕ - биссектриса) KA=KC (по условию задачи) Сторона КЕ - общая. Значит ΔАКЕ=ΔСКЕ по двум равным сторонам и углу между ними (первый признак)
3.∠BAC смежный с ∠1, значит он равен 180°-106°=74°
∠BCA=∠BAC (в равнобедренном треугольнике углы при основании равны)
∠BCA=74°
В равнобедренном треугольнике медиана является высотой, значит ∠BDC=90°
4. У этих треугольников ADC и ABC одна сторона (AC) общая и прилежащие к ней углы равны между собой (по условию задачи), значит треугольники равны. (второй признак).
Стороны DC и BC равны, так как ΔADC=ΔABC
В нашем случае α = 150°. Sin150=Sin(180-30)=Sin30=1/2.
Итак, S=(1/2)*a²*Sinα = (1/2)*a²*(1/2)=81. Отсюда а=√(81*4)=18.
ответ: боковая сторона равна 18.