i hope this helps you
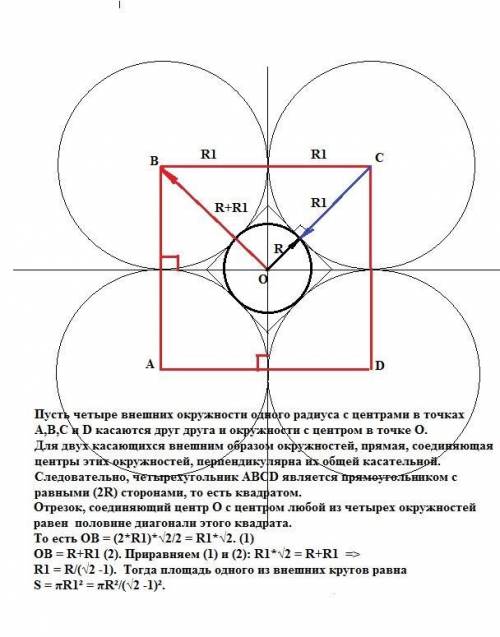
Пусть четыре внешних окружности одного радиуса с центрами в точках А,В,С и D касаются друг друга и окружности с центром в точке О.
Для двух касающихся внешним образом окружностей, прямая, соединяющая центры этих окружностей, перпендикулярна их общей касательной. Следовательно, четырехугольник АВСD является прямоугольником с равными (2R1) сторонами, то есть квадратом. Отрезок, соединяющий центр О с центром любой из четырех окружностей равен половине диагонали этого квадрата.
То есть ОВ = (1/2)*(2*R1)*√2= R1*√2. (1)
ОВ = R+R1 (2). Приравняем (1) и (2): R1*√2 = R+R1 =>
R1 = R/(√2 -1). Тогда площадь одного из внешних кругов равна
S = πR1² = πR²/(√2 -1)². Это ответ.
Если принять приближенное значение π ≈ 3,14, а √2 ≈ 1,41 то S ≈ 18,47*R² ед².
формула длины дуги сектора
т.е. длина окружности делится на ее градусную меру и умножается на величину угла сектора.
по условию •α=2π, откуда
формула площади кругового сектора s=•α, т.е. площадь полного круга делится на его градусную меру и умножается на градусную меру сектора.
подставим в формулу площади найденное из длины дуги значение r:
по условию π•360°/α=6π ⇒
α=60°⇒ r=360°: 60°=6 см
проведем биссектрису он угла сектора и к точке её пересечения с окружностью проведем касательную . продлим стороны угла сектора до пересечения с касательной в т.а и в.
∆ аов - равносторонний с высотой он=r=6
радиус вписанной в правильный треугольник окружности равен 1/3 его высоты.
r=6: 3=2
c=2πr=4π