MB= AB/2
BC/AB=1/2 <=> BC= AB/2 =MB
△BMC - равнобедренный.
∠BMC=∠BCM
Аналогично ∠AMD=∠ADM
∠A= 180°-∠AMD-∠ADM =180°-2∠AMD
∠B= 180°-∠BMC-∠BCM =180°-2∠BMC
Cумма односторонних углов при параллельных прямых равна 180°.
∠A+∠B=180° <=>
180° -2∠AMD +180° -2∠BMC =180° <=>
∠AMD+∠BMC =180°/2 =90°
∠CMD= 180°-∠AMD+∠BMC =180°-90° =90°
ИЛИ
Средняя линия MN делит ABCD на два равных параллелограмма. Основания ABCD равны половинам его сторон, следовательно BMNC и AMND - ромбы. Диагонали ромба являются биссектрисами его углов.
∠CMD =∠CMN+∠DMN =∠BMN/2+∠AMN/2 =180/2 =90.
Объяснение:
Так как 1 острый угол в нем 60 градусов, то 2 угол в треугольнике равен 90-60=30 градусов ( сумма острых углов 90) . А по правилу, сторона, против угла в 30 градусов, равна половине гипотенузы. Гипотенуза тут - это диагональ. (НО только в нашем случае) Диагональ = 10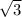
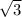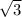Так что половина гипотенузы, то есть меньшая сторона треугольника (и прямоугольника в том числе) равна 0,5*10 =5 ( это одно и тоже, что и 10 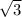: 2 )
А далее нам идет в теорема Пифагора. Круто)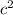 
=
+
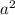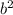, где c- гипотенуза, а и b - катеты. нам неизвестно b.
подставляем
=
- 
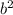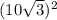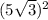
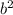= 100*3 - 25*3
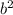= 300 - 75
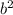=225
b= 15
А теперь можно найти площадь. S=A*B=15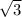*5 =75
ОТВЕТ: 15м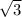, 5м, 75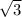 
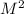
Надеюсь Объяснила суть решения.
