угол D=60°, угол С=90°, угол А=30°, угол С=30° и угол В=120°
Объяснение:
Проведенная диагональ АС делит этот параллелограмм АВСD на два треугольника: равнобедренный треугольник АВС и прямоугольный треугольник АСD.
Так как АСD прямоугольный треугольник, то угол С=90°.Итак у нас есть угол D(60°) и угол С(90°), находим угол А. Так как сумма углов треугольника равна 180°, получаем: 180°-уголD(60°)-уголС(90°)=30° -угол А. Итак мы нашли все углы прямоугольного треугольника АСD.
Перейдем к треугольнику АВС. Так как угол А=30°, то и угол С тоже будет 30° так как в равнобедренном треугольнике углы при основании равны. Получаем что угол А=30° и угол С=30°. И так как сумма углов треугольника равна 180°, получаем: 180°-уголА(30°)-уголС(30°) =120° -угол В.
Задача решена.
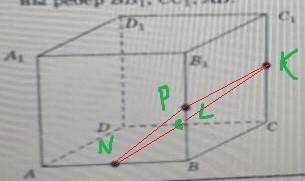
Чтобы построить сечение, проведем на нижней грани куба (см. рисунок) прямую NP║ВС, где N - середина АВ, P - середина DC. Затем соединим между собой точки N, L, K, P. В сечении получится прямоугольник NLKP.
Его площадь равна: S = NL * LK = 0,5 * AB₁ * BC = 0,5 * √2 * 1 =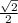 
.
AB₁ - диагональ квадрата, которая вычисляется как гипотенуза в равнобедренном прямоугольном треугольнике с катетами, равными единице. NL - средняя линия треугольника AB₁В.
ответ: площадь сечения равна 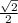квадратных единиц.
PS. На нормальном чертеже отрезки NP и KP нужно изображать пунктирными линиями, ибо они скрыты от наблюдателя снаружи куба.
∡ВОА=180°-∡АОС (смежные углы)
∡ВОА=180°-140°=40°
Рассмотрим ΔВОА
∡ВОА=40° ; ∡ОАВ=∡АВО=х (углы при основании равнобедренного треугольника равны; возьмем неизвестные углы за икс)
Сумма углов в треугольнике ΔВОА равна 180°
∡ОАВ+∡АВО+∡ВОА=180°
х+х+40°=180°
2х=140⇒х=70° (∡ОАВ=∡АВО=70°)
∡АВО=∡В=70°
Рассмотрим ΔАОС
∡АОС=140° ; ∡ОАС=∡ОСА=х (углы при основании равнобедренного треугольника равны; возьмем неизвестные углы за икс)
Сумма углов в треугольнике ΔАОС равна 180°
∡АОС+∡ОАС+∡ОСА=180°
140°+х+х=180°
2х=40⇒х=20° (∡ОАС=∡ОСА=20°)
∡ОСА=∡С=20°
∡А=∡ОАС+∡∡ОАВ=20°+70°=90°
∡А=90°
ответ: ∡А=90°; ∡С=20°; ∡В=70°