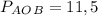 см
см
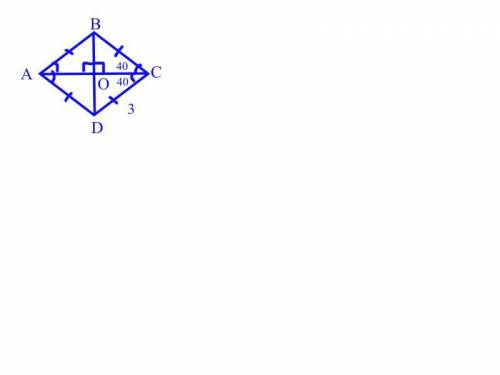
∠AOB=90°
∠ABO=50°
∠BAO=40°
Объяснение:
Дано: ABCD - ромб
CD = 3 см
AC = 9 см
BD = 8 см
∠C = 80°
Найти: PΔ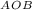 = ?
= ?
∠AOB=?
∠ABO=?
∠BAO=?
Решение: т.к ABCD - ромб, то у него все стороны равны ⇒ CD=BC=AB=AD=3 см
Диагонали ромба точкой пересечения делятся пополам: BO=OD=8/2=4 см; AO=OC=9/2=4,5 см
Противолежащие углы ромба равны ⇒ ∠C=∠A=80°, но т.к диагонали ромба являются биссектрисами его углов, то ∠OAD=∠BAO=80/2=40°
Диагонали ромба пересекаются под прямым углом ⇒ ∠AOB=90°
В ΔABO - прямоугольном, найдем ∠ABO. Сумма острых углов в прямоугольном треугольнике = 90°
∠ABO+∠BAO=90; ∠ABO=90-∠BAO; ∠ABO=90-40; ∠ABO=50°
Периметр - сумма длин всех сторон, тогда 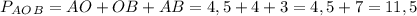 см
см
1.Углы альфа и бетта вписанные, значит они равны половине дуги на которую опираются, следовательно дуга соответствующая углу альфа равна 21*2=42(град), а дуга соответствующая углу бетта 49*2=98(град).
Найдем градусную меру дуги соответствующую углу х, 360-(180+98+42)=40, значит угол х=1/2*40=20(град)
ответ: 20град.
2.2х+3х+4х=180
9х=180
х=20
20*2=40(1-ый угол)
20*3=60(2-ой угол)
20*4=80(3-ий угол)
Проверка:
40+60+80=180
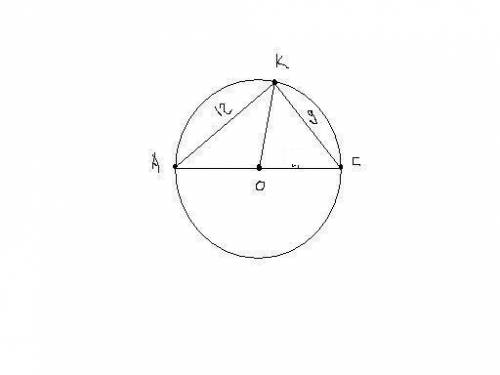
3.В треугольнике АКС угол К-прямой=90 градусов. Т.к Хорды окружности АК и КС построены из одной точки К на концы диаметра. Отсюда по тореме пифагора АС²=АК²+КС²
АС²=12²+9²=225
АС=√225=15
Радиус равен 15/2=7,5 (рисунок внизу)