Чтобы найти объем прямоугольного параллелепипеда нужно перемножить его высоту, ширину и длину. То есть
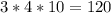
ОТВЕТ №1: Объем прямоугольного параллелепипеда равен 120 см²
Чтобы найти площадь основания конуса, нужно найти радиус. Если образующая наклонена под углом в 60°, то высота конуса равна половине ее длине (по свойству прямоугольного треугольника).
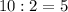
Чтобы найти радиус нужно воспользоваться теоремой Пифагора
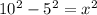
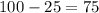
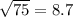 (примерно)
(примерно)
Теперь мы распологаем всеми значениями для вычисления объема
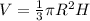
Подставляем значения
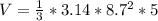

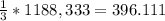
ОТВЕТ №2: Объем конуса равен примерно 396.111 см²
Треугольник СНВ - прямоугольный, ⇒ ∠НСВ=60°
СН противолежит углу 30° ⇒
СН=СВ:2 по свойству катета против угла 30°
Так как и СD=СВ:2, СН=СD⇒
треугольник НСD -равнобедренный.
Т.к. угол НСD =60°, углы при основании НD равны. Т,е. СНD=СDН=60°
Следовательно, треугольник СНD- равносторонний, НD=СН
Угол АСН=105°-60°=45°
Отсюда угол САН=90°-45°=45°
Δ АСН- равнобедренный, АН=СН=НD
Угол АНD=90°+60°=150°
Угол DАН=(180°-150°):2=15° ⇒
Угол ВАD=15°
-------
Для наглядности на приложенном рисунке все равные углы обозначены одинаковым цветом.