конус
S осн = 16п см²
S осев сеч = 12 см²
Найти:S бок поверхности - ?
Решение:S осн = пR² = 16п см²
R = √16 = 4 см
Осевое сечение данного конуса (если секущая плоскость проходит через ось конуса) - равнобедренный треугольник.
Так как △ВРА - равнобедренный => Н (или РО) - высота, медиана, биссектриса.
=> BO = OA = 4 см,(они и есть R) так как РО - медиана.
=> BA = 4 * 2 = 8 см (это и диаметр D)
S треугольника = (1/2ВА) * Н (или РО) = 12 см²
=> Н (или РО) = S треугольника/(ВА * 1/2)
Н (или РО) = 12/(8 * 1/2) = 3 см
△ВРО и △АРО - прямоугольные, так как РО - высота.
По теореме Пифагора найдём образующую l (или BP, PA):
с² = а² + b²
c = √a² + b²
c = √3² + 4² = √9 + 16 = √25 = 5 см
S бок поверхности = пRl
S бок поверхности = п * 4 * 5 = 20п см²
ответ: 20п см²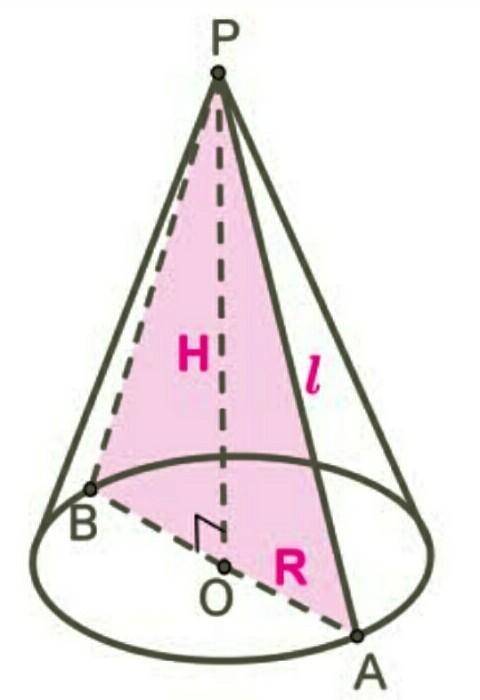
Рисунок во вложении, хотя можно вполне обойтись без него.
1) Найдем вторую сторону основания параллелепипеда из формулы площади основания. Т.к. он прямоугольный, основание - прямоугольник.
S=a*8=40
а=S:8=40:8=5 см
2) Найдем высоту параллелепипеда из формулы объема.
V=S·h
h=V:S
h=240:40=6cм
Площадь боковой поверхности равна произведению высоты на периметр основания:
Sбок=h·2(a+b)
Sбок=6·2·(8+5)=156 см²
Площадь полной поверхности параллелепипеда равна сумме площадей двух его оснований и боковой поверхности:
Sполн= 2·Sосн +Sбок
Sполн=80+156=236 см²
Диагональ можно найти с теоремы Пифагора ( см. рисунок)
Для этого нужно сначала вычислить диагональ основания АС.
Диагональ АС1 параллелепипеда равна
АС1=√(АС²+С1С²)
Можно воспользоваться теоремой:
Квадрат диагонали параллепипеда равен сумме квадратов трех его линейных измерений.
АС1²=АВ²+ВС²+С1С²=8²+5²+6²=125
АС1=√125=5√5 см
-----------------------------------------
№2
Объем прямоугольного параллелепипеда равен произведению высоты на площадь его основания или произведению трех его измерений. Что одно и то же.
V=a·b·c
Об основании известно, что его периметр Р равен 40 см.
Р=2(а+b)
Ни а, ни b не известны, но их длину можно найти.
Пусть ширина основания а, тогда его длина ( по условию) а+4
40=2·(а+а+4)=2а+2а+8=4а+8
4а=40-8=32 см
а=8 см
b=8+4=12 см
Высоту найдем из площади боковой поверхности, которая равна произведению высоты на периметр основания:
Sбок=hP
h=Sбок:Р
h=400:40=10 см
V=a·b·c=8·12·10=960 см³
