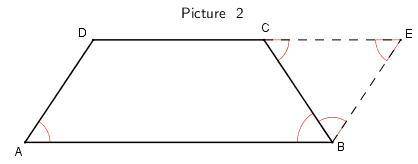
Предоставлю точно также два решения только другой метод(более рационален). Из вершины D продлим сторону до пересечения на продлении стороны BC, так что AB ║ DE, т.е. ABED — параллелограмм.
∠A = ∠E = 60° (противоположные углы у параллелограмма равны)
Так как AB = CD ⇒ ED = CD ⇒ ∠ECD = ∠CED = ∠CDE = 60°, т.е. треугольник CDE — равносторонний ⇒ CD = CE = ED = 32
Тогда AD = BC + CE = 20 + 32 = 52
P = 20 + 32 + 32 + 52 = 136
Рисунок 2.
Аналогично решению из рисунка 1, достроим до параллелограмма ADEB, AD ║ EB, мы имеем что ΔCEB - равносторонний, т.е. CE = CB = EB = 20, тогда CD = AB - CE = 32 - 20 = 12.
P = 12 + 20 + 20 + 32 = 84


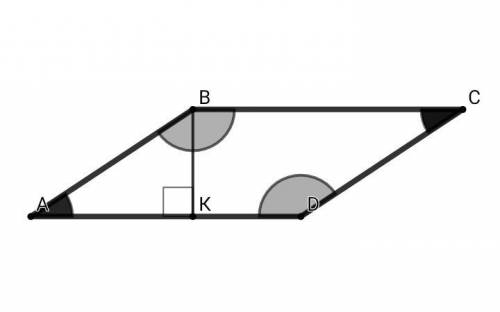
Полное условие задания:
В параллелограмме ABCD, из вершины тупого угла В Δ ABC проведен перпендикуляр BK к стороне AD (K ∈ AD) и BK = 0,5•AB. Найдите углы параллелограмма.
Параллелограмм - это четырёхугольник, у которого противолежащие стороны попарно параллельны, а углы попарно равныВК = АВ/2
В прямоугольном ΔАВК: катет ВК, лежащий против ∠ А, равен половине гипотенузы АВ ⇒ ∠А = 30°
∠ABC + ∠BAD = 180° - как односторонние углы при BC || AD и секущей АВ ⇒ ∠ABC = 180° - ∠BAD = 180° - 30° = 150°
∠А = ∠С = 30° , ∠B = ∠D = 150°
ответ: 30° , 150° , 30° , 150°
Угло при нижнем основании равнобедренной трапеции меньше 90°, а при верхнем больше 90°, поэтому ∠A = 60° - угол основания.
Нам неизвестно какая сторона боковая, известно только то, что они смежные. Поэтому решим два варианта.
1. AB - нижнее основание.
H₁, H₂ ∈ AB; DH₁ , CH₂ ⊥AB ⇒ DH₁ ║ CH₂
ΔADH₁ = ΔCBH₂ - по гипотенузе и острому углу т.к. трапеция равнобедренная.
AH₁ = H₂B - как соответственные стороны равных Δ.
∠H₂CB = 90° - ∠CBH₂ = 90° - 60° = 30° - как острые улг. в прямоугольном Δ.
H₂B = BC/2 = 20/2=10 - как катет лежащей напротив угла в 30° в прямоугольном Δ.
H₁H₂ = 32 - 10*2 = 12 = т.к. DH₁ ║ CH₂ и DH₁ = CH₂ - как соответственные стороны равных Δ.
P - периметр.
P = AB+ 2BC + CD = 32 + 40 + 12 = 84.
ответ: 84.
2. AB - боковая сторона.
H₁, H₂ ∈ AD; BH₁ , CH₂ ⊥AD ⇒ BH₁ ║ CH₂ ⇒ BH₁ = CH₂ - как параллельные отрезки заключённые между параллельными прямыми, поэтому BCH₂H₁ - прямоугольник ⇒ H₁H₂ = BC = 20.
ΔABH₁ = ΔCDH₂ - по гипотенузе и острому углу т.к. трапеция равнобедренная.
AH₁ = H₂D - как соответственные стороны равных Δ.
∠ABH₁ = 90° - ∠BAH₁ = 90° - 60° = 30° - как острые улг. в прямоугольном Δ.
AH₁ = AB/2 = 32/2=16 - как катет лежащей напротив угла в 30° в прямоугольном Δ.
BC = AD т.к. BH₁ ║ CH₂ и BH₁ = CH₂ - как соответственные стороны равных Δ.
AD = 20 + 16·2 = 52
P - периметр.
P = 2AB + BC + DA = 64 + 20 + 52 = .
ответ: 136.