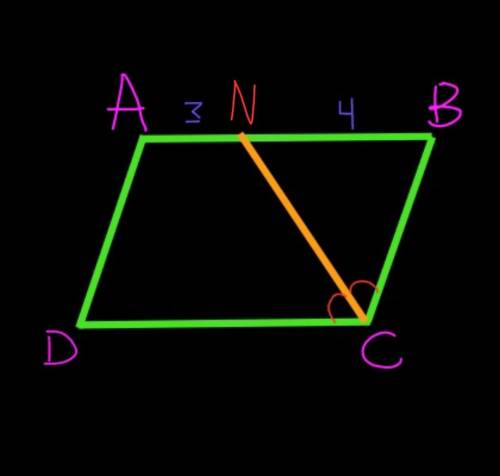
№1 первый рисунок, на нем изображено то что дано.
Так как АВСD – параллелограмм, то АВ||CD, тогда угол DCN = угол
BNC как накрест-лежащие при паралельных прямых AB u CD и секущей CN.
CN – биссектриса по условию, значит угол DCN= угол BCN.
Исходя из равенств: угол BNC= угол DCN= угол BCN. Получим что ∆BNC – равнобедренный с основанием CN, так как углы при его основании равны.
У равнобедренного треугольника боковые стороны равны, следовательно BC=BN=4 см
Периметр параллелограмма это сумма двух его смежных сторон, умноженная на два. Тоесть:
P=(ВС+АВ)*2= (ВС+AN+BN)*2= (4+3+4)*2=22 см.
ответ: 22 см
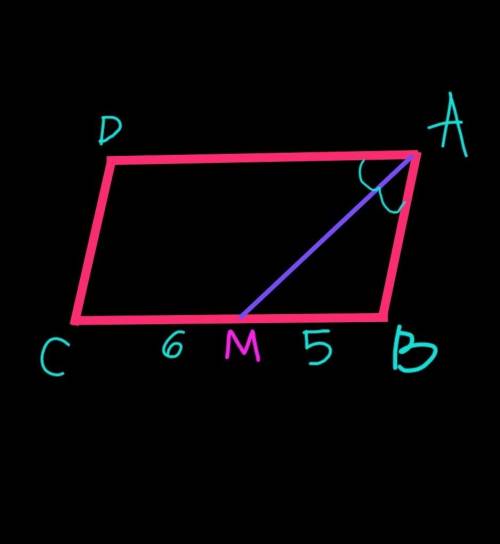
№2 второй рисунок, на нем изображено то что дано
Та что е ABCD – параллелограмм, то АD||BC, тогда угол DAM= угол BMA как накрест-лежащие при паралельных прямых AD и BC и секущей АМ.
АМ – по условию биссектриса, значит угол DAM= угол BAM.
Исходя из ранее найденного: угол DAM= угол АМВ= угол ВАМ.
Тогда получим что, ∆ВАМ – равнобедренный с основанием АМ, так как углы при основании равны.
АВ=ВМ как боковые стороны равнобедренного треугольника, тогда АВ=5 см.
Периметр параллелограмма это сумма двух его смежных сторон, умноженная на два. Тоесть:
Р=(АВ+ВС)*2=(АВ+ВМ+СМ)*2= (5+5+6)*2= 32 см.
ответ: 32 см
1)Два треугольника называются подобными, если их углы соответственно равны
1) да ; 2) нет
Вспомним 1-й признак подобия:
если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2)Любые два прямоугольных и равнобедренных треугольника подобны.
1) нет ;2) да
Верно. По первому признаку. Углы при основании равны 45°,а напротив основания 90°
3)Любые два прямоугольных треугольника подобны.
1) да 2) нет
В таких треугольниках мы можем утверждать только о равенстве одного угла-прямого. Ни для одного признака подобия этого недостаточно
Неверно
4 )Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны
1) да 2) нет
Более подходящие признаки
2-й -если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны. Равенство углов нам не дано. Утверждать не можем
3-й -: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны. Нам даны по 2 стороны. Утверждать не можем
5)Если два треугольника подобны, то их соответствующие стороны равны
1) да; 2) нет
3-й признак: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.
6)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
1) да ; 2) нет
Теорема верная.
7)Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
1) да ; 2) нет
Это первый признак равенства. А,равные треугольники подобны
8)Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.
1) да ; 2) нет
Вспомним 1-й признак подобия:
если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
По теореме пифагора половинина основания равна (корень из 17 в кв - 8 в кв )= 15*2= 30