1) Если точка А лежит между точками В и С, тогда АВ + АС = ВС. Проверим:
АВ + АС = 4,3 + 7,5 = 11,8 (см)
ВС = 3,2 (см)
11,8 см ≠ 3,8 см ⇒ точка А не может лежать между точками В и С.
2) Если точка С лежит между точками А и В, тогда АС + ВС = АВ. Проверим:
АС + ВС = 7,5 + 3,2 = 10,7 (см)
АВ = 4,3 (см)
10,7 см ≠ 4,3 см ⇒ точка С не может лежать между точками А и В.
3) Если точка В лежит между точками А и С, тогда АВ + ВС = АС. Проверим:
АВ + ВС = 4,3 + 3,2 = 7,5 (см)
АС = 7,5 (см)
7,5 см = 7,5 см ⇒ точка В лежит между точками А и С.
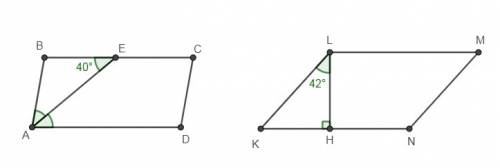
а) Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ⇒ ∠ВАЕ = ∠ВЕА = 40°
∠А = 2∠ВАЕ = 2 * 40 = 80° (так как АЕ - биссектриса ∠А)
Сумма соседних углов параллелограмма равна 180° ⇒
∠В = 180 - ∠А = 180 - 80 = 100°
Противоположные углы параллелограмма равны ⇒
∠С = ∠А = 80°
∠D = ∠В = 100°
ответ: 80°; 80°; 100°; 100°.
-------------------------------------------------------------------------
б) ΔKLH - прямоугольный ⇒ ∠К = 90 - 42 = 48°
Сумма соседних углов параллелограмма равна 180° ⇒
∠L = 180 - ∠K = 180 - 48 = 132°
Противоположные углы параллелограмма равны ⇒
∠M = ∠K = 48°
∠N = ∠L = 132°
ответ: 48°; 48°; 132°; 132°.
ABCD - квадрат
AB = a см
Найти:
AB/AC = ?
Решение:
Диагональ делит квадрат на два равных равнобедренных прямоугольных треугольника, рассмотрим один из них:
Треугольник равнобедренный, значит острый угол = 45,
cos 45 = √2/2
Составляем пропорцию:
x/y=√2/2 (x - катет, у - гипотенуза)
√2у=2х
у=2/√2x
Избавляемся от иррациональности в знаменателе:
y=√2x
Значит,
AB/AC = x/√2x=1/√2