Сдвумя ! с рисунками и полным ответом, ! 1. докажите, что если плоскость y пересекает одну из параллельных плоскостей альфа и бета, то она пересекает и другую плоскость. 2. докажите, что через точку а, не лежащую в плоскости альфа, проходит плоскость, параллельная плоскости альфа, и притом только одна.

👇

Ответ:

ayratka2

19.12.2022

Допустим, прямая не пересекает плоскость бета, а параллельна ей. Тогда все точки этой прямой должны находиться на равном удалении от плоскости бета (иначе один из концов пряой приблизится к плоскости бета и пересечет ее) . Одна точка, точка пересечения прямой с плоскостью альфа, находится на том же расстоянии от плоскости бета, что и плоскость альфа. Следовательно все остальные точки прямой находятся на таком же расстоянии, т. е. лежат в плоскости альфа, значит вся прямая долна лежать в плоскости альфа. Но по условию прямая не лежит в плоскости альфа, а пересекает ее. Таким образом она не может быть параллельна плоскости бета и пересечется с ней.

2Проведем в плоскости α две пересекающиеся прямые a и b, а через точку А проведем прямые a1 и b1, соответственно параллельные прямым а и b. Рассмотрим плоскость β, проходящую через прямые a1 и b1. Плоскость β — искомая, так как она проходит через точку A и по признаку параллельности двух плоскостей параллельна плоскости α.Докажем теперь, что β — единственная плоскость, проходящая через точку А и параллельная плоскости &alpha. В самом деле, любая другая плоскость, проходящая через точку А, пересекает плоскость β, поэтому пересекает и параллельную ей плоскость a

4,7(68 оценок)

Открыть все ответы

Ответ:

lanv

19.12.2022

Для решения нам нужно найти высоту

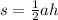
$s = \frac{1}{2} ah$

Вот формула площади треугольника. Но так как треугольник прямоугольный, то высота=катет

Здесь используем формулу Пифагора

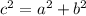
${c}^{2} = {a}^{2} + {b}^{2}$

с — гипотенуза, a и b - катеты

Гипотенуза у нас известна, значит используем обратную формулу

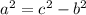
${a}^{2} = {c}^{2} - {b}^{2}$

a²=20²-15²=400-225=175

a²=175

Так как в таблице квадратов такого числа нет, значит

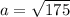
$a = \sqrt{175}$

Мы нашли катет, тобишь высоту.

Далее пользуемся формулой площади.

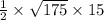
$\frac{1}{2} \times \sqrt{175} \times 15$

(a — высота, b — основание, по свойствам прямоугольного треугольника)

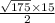
$\frac{ \sqrt{175} \times 15 }{2}$

Не думаю, что нужно преобразрвывать, ибо там получится число с большим количеством числел после запятой, если конкретно, то:

99,215674164922147143810590761472265964134

Так что, думаю, лучше оставить формулой (где с дробью)

Можно также ещё преобразовать корень:

(не могу дополнить с формулой, увы, так что "V" = корень, ' — где он заканчивается)

Разбиваем корень на два множителя, один из которых можно будет вычислить.

V175' =V25' × V7`= 5V7'

Пять корней из семи. Значит в том ответе с дробью в числителе можно написать 5V7×15

4,4(30 оценок)

Ответ:

Murew

19.12.2022

R≅5,04

H≅5,04

Объяснение:

Объём цилиндра :

(1) V = πR²H,

где R - радиус цилиндра, H - высота цилиндра.

Площадь полной поверхности цилиндра:

(2) S = πR² + 2πRH

Выразим из формулы (1) высоту цилиндра и подставим значение в формулу (2):

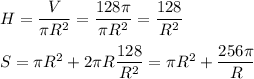
$H= \dfrac{V}{\pi R^{2} } =\dfrac{128\pi }{\pi R^{2} } =\dfrac{128}{R^{2} } \\\\S = \pi R^{2} +2\pi R\dfrac{128}{R^{2} } = \pi R^{2} + \dfrac{256\pi }{R}$

Найдём минимум этой функции по переменной R. Для этого вычислим производную и определим критические точки.

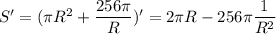$S' = (\pi R^{2} +\dfrac{256\pi }{R} )' = 2\pi R-256\pi \dfrac{1}{R^{2} }$ .

S' = 0,

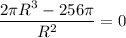
$\dfrac{2\pi R^3-256\pi }{R^{2} } = 0\\$

Если R = 0, то производная не существует.

$2\pi (R^3-128)=0\\\\R^3 = 128\\\\R=\sqrt[3]{128}$

R≅ 5.04

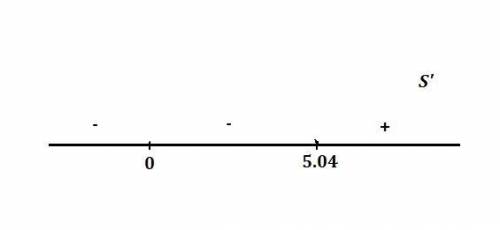
Отметим эти значения на координатной прямой и oпределим знак производной на трёх полученных числовых интервалах. (Cм.рис)

Известно, что в точке минимумa производная меняет знак с минусa на плюс. Соответственно, наименьшее количество материала можно получить, если радиус основания цилиндра R=5,04

Вычислим соответствующую высоту цилиндра:

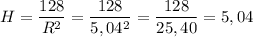
$H = \dfrac{128}{R^{2} } =\dfrac{128}{5,04^{2} } =\dfrac{128}{25,40} = 5,04$