Пусть дан один равнобедренный треугольник и второй равнобедренный треугольник АВС с равными углам при основаниях, следовательно, и третий угол при вершине одного треугольника равен третьему углу второго.
Эти треугольники подобны. В подобных треугольниках все их элементы пропорциональны, следовательно, точка пересечения биссектрисы угла при основании с высотой второго треугольника делит ее в том же отношении, что в первом, т.е. 5:3
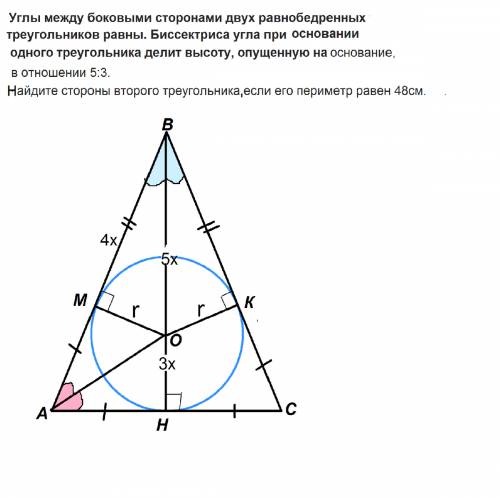
Высота ВН равнобедренного треугольника, проведенная к основанию, является и биссектрисой и медианой. АН=НС.
Имеем две биссектрисы треугольника АВС, которые пересекаются в некой точке О. Точка О пересечения биссектрис треугольника АВС является центром вписанной в него окружности.
Из точки О проведем перпендикуляры ОМ и ОК к боковым сторонам треугольника. М, К и Н - точки касания окружности и сторон треугольника.
ОМ=ОК=ОН= радиусу вписанной окружности.
Пусть коэффициент отношения отрезков высоты равен х.
Тогда ВО=5х, ОН=3х, ОМ=ОК=3х
Треугольники ВОМ и ВОК - египетские,т.к. катет и гипотенуза относятся как 3:5 ⇒
ВМ=ВК=4х ( можно проверить по т.Пифагора)
ВН=3х+5х=8х
Треугольники ВМО и ВНА - подобные, т.к. оба прямоугольные и имеют общий острый угол. Следовательно, треугольник ВНА тоже египетский, и из отношения сторон такого треугольника следует
АВ=10х, АН=6х. Или из подобия треугольников через отношение сходственных сторон
ВН:ВМ=АН:ОМ
ВН=3х+5х=8х
8х:4х=АН:МО
АН:МО=2
АН=6х
АВ=ВС=5*2=10х
ВН - медиана, поэтому
АС=6х+6х=12х
Периметр треугольника равен АВ+ВС+АС=48
Р=10х+10х+12х=32х
32х=48
х=1,5 см
АВ=ВС=1,5*10=15 см
АС=1,5*12=18 см
Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
а) По теореме Пифагора:
AC = √(AB² - BC²) = √(17² - 8²) = √(289 - 64) = √225 = 15
sin∠A = BC / AB = 8/17 sin∠B = AC / AB = 15/17
cos∠A = AC / AB = 15/17 cos∠B = BC / AB = 8/17
tg∠A = BC / AC = 8/15 tg∠B = AC / BC = 15/8
б) По теореме Пифагора:
АВ = √(BC² + AC²) = √(21² + 20²) = √(441 + 400) = √841 = 29
sin∠A = BC / AB = 21/29 sin∠B = AC / AB = 20/29
cos∠A = AC / AB = 20/29 cos∠B = BC / AB = 21/29
tg∠A = BC / AC = 21/20 tg∠B = AC / BC = 20/21
в) По теореме Пифагора:
АВ = √(BC² + AC²) = √(1² + 2²) = √(1 + 4) = √5
sin∠A = BC / AB = 1/√5 sin∠B = AC / AB = 2/√5
cos∠A = AC / AB = 2/√5 cos∠B = BC / AB = 1/√5
tg∠A = BC / AC = 1/2 tg∠B = AC / BC = 2
г) По теореме Пифагора:
ВС = √(АВ² - AC²) = √(25² - 24²) = √(625 - 576) = √49 = 7
sin∠A = BC / AB = 7/25 sin∠B = AC / AB = 24/25
cos∠A = AC / AB = 24/25 cos∠B = BC / AB = 7/25
tg∠A = BC / AC = 7/24 tg∠B = AC / BC = 24/7
MN II CD
KN II BD
значит, плоскость BCD II KMN
KM=1/2 BC, т.к. КМ – средняя линия Δ АВС
MN=1/2 CD, т.к. МN – средняя линия Δ АСD
NK=1/2 DB, т.к. NК – средняя линия Δ BАD
S Δ BCD = 2* S Δ KMN = 2*36=72 м^2