Объяснение:
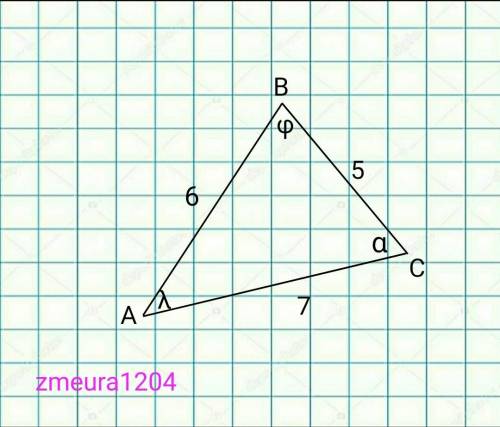
Дано: ΔАВС.
АВ = 5м; ВС = 6м; АС = 7м.
Найти: cos∠A; cos∠B; cos∠C
Для решения воспользуемся теоремой косинусов:
a² = b² + c² - 2 bc · cos∠A
1. Найдем cos∠A:
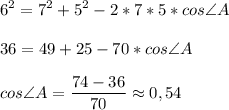
2. Найдем cos∠B:
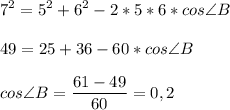
3. Найдем cos∠C:
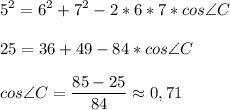
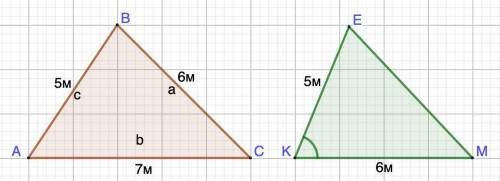
2) Дано: ΔКЕМ.
КЕ = 5 м; КМ = 6 м; sin∠K = 0,6
Найти: ЕМ
Воспользуемся теоремой косинусов. Но для этого нам нужен косинус, а нам дан синус.
Выразим косинус из основного тригонометрического тождества:
sin²α + cos²α = 1
Тогда имеем:
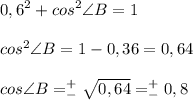
Так как в условии не сказано, острый это угол или тупой, то рассмотрим 2 варианта:
1. cos∠B = 0,8
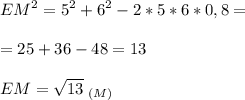
2. cos∠B = -0,8
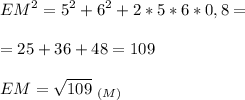
Объяснение:
109)1)
cos<λ=(AB²+AC²-BC²)/(2*AB*AC)=
=(6²+7²-5²)/(2*6*7)=(36+49-25)/84=
=60/84=5/7
cos<φ=(AB²+BC²-AC²)/(2*AB*BC)=
=(6²+5²-7²)/(2*6*5)=(36+25-49)/60=
=12/60=1/5
cos<α=(ВС²+СА²-АВ²)/(2*ВС*СА)=
=(5²+7²-6²)/(2*5*7)=(25+49-36)/70=
=38/70=19/35
ответ: cos<α=19/35; cos<λ=5/7; cos<φ=1/5
109)2)
Дано:
Треугольник
а=5м сторона
b=6м сторона
sin<α=0,6, где <α- угол между а;b
c=?
Решение
Тригонометрическое тождество
sin²α+cos²α=1
cos<α=√(1-sin²α)=√(1-0,6²)=√(1-0,36)=
=√0,64=0,8.
Теорема косинусов
c=√(a²+b²-2*a*b*cos<α)=√(5²+6²-2*5*6*0,8)=√(25+36-48)=√13м третья сторона треугольника
ответ: √13 м
Ищем площадь 1/2*9*6=27 см².