ответ: а) <А=30°, <В=120°, <С=30°; б) АВ=ВС.
Дано:
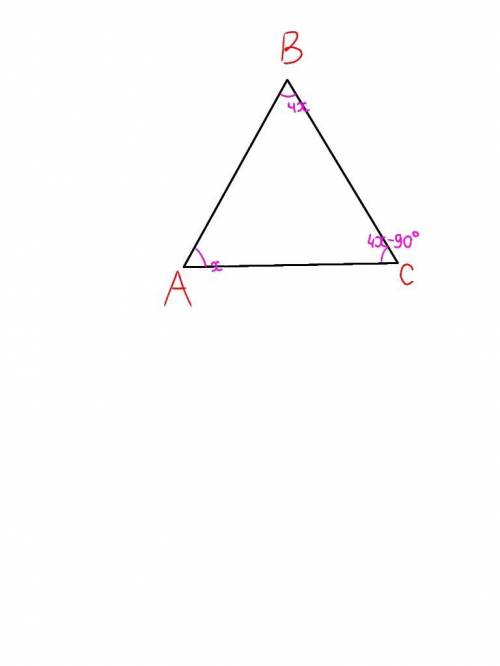
∆ ABC
угол А в 4 раза < угла В
угол С на 90° < угла В
<А, <В, <С - ?
а) 1) Пусть угол А - х, тогда угол В - 4х, а угол С = 4х-90°. Составим и решим уравнение:
х+4х+(4х-90) = 180 (по сумме углов треугольника)
х+4х+4х-90 = 180
х+4х+4х = 180+90
9х = 270
х = 270/9
х = 30 → угол А = 30°.
2) Тогда угол В = 4*30° = 120°.
3) Значит, угол С = 120° - 90° = 30°
б) Следовательно, АВ = ВС, тк ∆АВС - равнобедренный - тк <А = <С = 30° (по свой-ву р/б треугольника углы при основании равны).
ответ: а) <А=30°, <В=120°, <С=30°; б) АВ=ВС.
и высоту ВD проведенную к ВС - эту часть задания я непоняла потмоучто ВD - высота проведённая к АС а вы написали к ВС как такую высоту провести непонятно
По поводу остального:
1) треугольник ВDС - прямоугольный нам известны гипотенуза = 13 и катет = 12 Найдем катет, то есть высоту ВD
ВD=корень(169-144)=корень(25)=5 см
2)треугольник АВD - прямоугольный, угол А=45 градусов по условию, а значит он и равнобедренный, тогда АD=5 см
3)АС=5+12=17 см
4)S=(АС*ВD)/2 = (17*5)/2= 85/2= 42.5 см^2
Возможно ошибаюсь, но думаю что решение такое)