EM=KR=8; MK=ER=10
Объяснение:
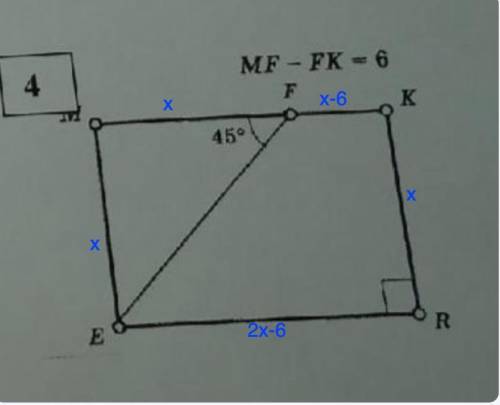
Дано: ЕМКR - прямоугольник
∠MFE=45°
MF-FK=6
P (ЕМКR)=36
Найти: стороны прямоугольника.
Пусть MF=x ⇒ FK=MF-6=x-6
Рассмотрим ΔEMF - прямоугольный
∠MFE=45°
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠MEF=45°
ΔEMF - равнобедренный (углы при основании равны)
⇒ EM=MF=x
Противоположные стороны прямоугольника равны.
EM=KR=x
MK=ER=x+(x-6)=2x-6
Периметр прямоугольника равен удвоенной сумме длин соседних сторон.
Р (ЕМКR)=2(х+2х-6)=2(3х-6)
36=2(3х-6)
3х-6=18
3х=24
х=8
⇒ EM=KR=8
MK=ER=2x-6=10
Відповідь:
Пояснення:
Щоб знайти периметр прямокутної трапеції, в яку вписано коло, треба знати її властивості. У такій трапеції 1) сума бокових сторін дорівнює сумі основ, 2) якщо точки дотику ділять бокову сторону на відрізки m i n, то r=√mn 3) менша бокова сторона дорівнює діаметру кола.
r=√18*8=12, отже менша бічна сторона = 12*2=24 см.
Більша бічна сторона = 8+18=26 см.
Сума бічних сторін=24+26=50 см.
Сума основ = сумі бічних сторін=50 см.
Периметр трапеції=50+50=100 см.
Відповідь: 100 см
Детальніше - на -