Расстояние от точки до плоскости равно длине отрезка, проведенного к ней перпендикулярно.
М удалена от каждой вершины треугольника, следовательно, проекции прямых, соединяющих её с вершинами треугольника АВС, равны радиусу описанной окружности., а М проецируется в центр О этой окружности.
∠ВАС- вписанный, ∠ВОС - центральный и равен 2•∠АОС=60° по свойству вписанных углов.
Тогда ∆ ВОС равносторонний, радиус описанной окружности равен R=ВС=8.
∆ ВОМ прямоугольный, гипотенуза МВ=17, катет ВО=8
По т.Пифагора ( её Вы уже знаете) МО=15 см.
По т.синусов
2R=ВС:sin30°= 8:0,5=16⇒
R=8
Нахождение МО описано в первом варианте.
Объяснение:
можно лучший ответ
ответ: 2688 см²
Объяснение:
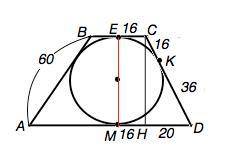
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны.
Для трапеции АВСD, в которую вписана окружность, BC+AD=AB+CD=60+16+36=112 см.
Стороны трапеции - касательные к вписанной окружности. Обозначим точки касания на ВС– Е, на СD - К, на AD-М. По свойству равенства отрезков касательных, проведенных из одной точки, СЕ=СК=16, DK=DM=36.
Соединим точки касания на основаниях отрезком ЕМ. Опустим высоту СН. МН=ЕС=16
DH=DM-CE=36-16=20.
По т.Пифагора СН=√(CD²-DH²)=√(52²-20²)=48 (см)
Площадь трапеции равна произведению полусуммы оснований на высоту.
S(ABCD)=0,5(BC+AD)•CH=0,5•112•48=2688 см².
=1/2АС, 1/2*1/2ВС*ВС=36, ВС=12