1) пусть стороны АВ=5, ВС=8 и АС=12 и стороны А1В1=15, В1С1=24 и А1С1=26, относятся как A1B1/AB=15/5=3 и т.д.
значит по третьему признаку подобия треугольники подобны
Свойства подобных треугольников Отношение площадей подобных треугольников равно квадрату коэффициента подобия
S1/S=3^2=9
2) Если угол при вершине равнобедренного треугольника равен 38°, то углы при основании будут равны = 71°. Значит два угла при основании одного треугольника равны двум углам при основании другого треугольника, т.е. они подобны по первому признаку подобия треугольников.
3) 1) AB=AD-BD=22-8=14; По теореме Фалеса AB:AC=BD:CE; AC=AB*CE:BD=14*10:8=17,5. 2) AE=AC+CE=8+10=18; Треугольники ADE и ABC подобны, АЕ:AC=DE:BC; DE=AE*BC:AC=18*4:8=9;
Для решения нам нужно найти высоту
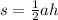
Вот формула площади треугольника. Но так как треугольник прямоугольный, то высота=катет
Здесь используем формулу Пифагора
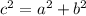
с — гипотенуза, a и b - катеты
Гипотенуза у нас известна, значит используем обратную формулу
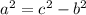
a²=20²-15²=400-225=175
a²=175
Так как в таблице квадратов такого числа нет, значит
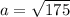
Мы нашли катет, тобишь высоту.
Далее пользуемся формулой площади.
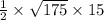
(a — высота, b — основание, по свойствам прямоугольного треугольника)
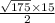
Не думаю, что нужно преобразрвывать, ибо там получится число с большим количеством числел после запятой, если конкретно, то:
99,215674164922147143810590761472265964134
Так что, думаю, лучше оставить формулой (где с дробью)
Можно также ещё преобразовать корень:
(не могу дополнить с формулой, увы, так что "V" = корень, ' — где он заканчивается)
Разбиваем корень на два множителя, один из которых можно будет вычислить.
V175' =V25' × V7`= 5V7'
Пять корней из семи. Значит в том ответе с дробью в числителе можно написать 5V7×15
Угол ВАС вписанный и опирается на дугу ВС, значит
∠ВАС = ∪BC/2 = x/2
Угол DCA вписанный и опирается на дугу AD, значит
∠DCA = ∪AD/2 = (x + 22)/2
Сумма углов треугольника равна 180°. Для треугольника АМС получаем уравнение:
120°+ x/2 + (x + 22)/2 = 180°
(2x + 22)/2 = 60°
x + 11° = 60°
x = 49°
∪BC = 49°