Стороны треугольника 60 см, 61 см, 11 см.найдите его площадь

Question

Геометрия: Стороны треугольника 60 см, 61 см, 11 см.найдите его площадь

ЕлизаветаАлис · Accepted Answer

Решение:
1) Найдем объем отсеченной части пирамиды.
Так как плоскость сечения находится на расстоянии 3 см от вершины пирамиды, ее высота равна 3 см.

Объем пирамиды равен произведению 1/3 на высоту и на площадь основания.

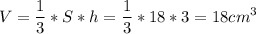
$\displaystyle V= \frac{1}{3}*S*h= \frac{1}{3}*18*3=18 cm^3$

2) Плоскоcть сечения параллельна основанию пирамиды, поэтому пирамиды подобны.
Объемы подобных фигур относятся как их коэффициенты подобия в кубе.

Найдем коэффициент подобия:

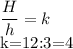
$\displaystyle \frac{H}{h}=k

k=12:3=4$

3) Значит отношение объемов фигур будет равно 4³=64

Найдем объем большой пирамиды

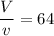
$\displaystyle \frac{V}{v}=64$

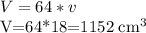
$\displaystyle V=64*v

V=64*18=1152 cm^3$

ответ Объем пирамиды 1152 см³