Пусть дан прямоугольник АВСД, с диагоналями АС и ВД - пересекающимися в точке О. Пусть угол АОВ = 60 град., тогда из неравенства треугольника следует, что напротив меньшего угла лежит мень шая сторона треугольника, т.к. углы АОВ и ВОС смежные, то угол ВОС = 120град., следовательно сторона АВ меньше стороны ВС.
в прямоугольнике диагонали пересекаюися и точкой пересечения делятся пополам (сво-во диагоналей прямоугольника), значит ВО=АО=5см, следовательно треугольник АОВ - равнобедренный, значит углы АВО и ОАВ равны по 60 град, а следовательно треугольник АОВ так же является равносторонним, значит АО=ОВ=АВ=5см.
ответ: 5см.
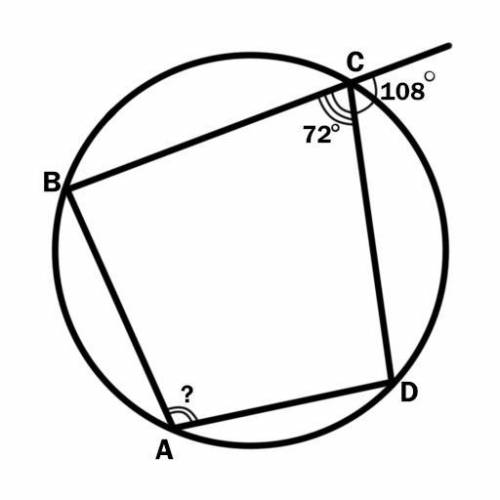
Найдите ∠BAD четырёхугольника ABCD, вписанного в окружность, если внешний ∠С четырёхугольника равен 108°.
- - -
Дано :
Четырёхугольник ABCD - вписанный в окружность.
Внешний ∠С = 108°.
Найти :
∠BAD = ?
Рассмотрим внешний ∠С и ∠BCD - смежные.
Сумма смежных углов равна 180°.Отсюда -
Внешний ∠С + ∠BCD = 180°
∠BCD = 180° - внешний ∠С
∠BCD = 180° - 108°
∠BCD = 72°.
Теперь рассмотрим ∠BCD и ∠BAD - противоположные.
Если в окружность можно вписать четырёхугольник, то сумма двух противоположных углов равна 180°.Отсюда -
∠BCD + ∠BAD = 180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 72°
∠BAD = 108°.
108°.
Треугольник, вершины которого - точка пересечения диагоналей и вершины меньшей стороны - равносторонний (равнобедренный с углом 60 градусов), поэтому меньшая сторона равна половине диагонали, то есть 5 см.