AK = CM
Объяснение:
Имеем углы KAB и MCB. Для начала нужно доказать что эти углы равны, а если эти углы будут равны, то и стороны этих углов тоже будут равны. Первое свойство равнобедренного треугольника гласит: углы при основании равнобедренного треугольника равны. Проведём медиану BD, которая будет делить данный треугольник на равные части. Т.к. углы BAD и BCD равны, то углы KAB и BAD, будут вертикальные, а значит равны. Углы MCB и BCD тоже будут вертикальные, а значит тоже равны между собой. А т.к. углы при основании равны и оба из них имеют равные прилежащие углы, то и углы KAB и MCB, тоже равны!
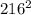
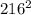
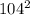
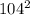
S = (a b c) / (4 R) также площадь равна S = 1/2 c h.
Следовательно, (a b c) / (4 R) = 1/2 c h
Так как треугольник равнобедренный, a = b = 5, R = 5; c - основание тр-ка.Сократим уравнение на величину "с" и подставим значения:(5*5) / (4*5) = 1/2 * h5/4 = 1/2 hh = 5/2 – высота треугольникаПо теореме Пифагора половина основания равна:1/2 с = √52 - (5/2)2 = √75/4 = √3*25/4 = 5/2 √3,Полное основание равно 2 * 5/2 √3 = 5√3Площадь треугольника будет равна:S = 1/2 * 5√3 * 5/2 = 25/4 √3