Сделайте рисунок к задаче. Он может выглядеть как угол комнаты - отрезки направлены в разные стороны.
Соедините концы отрезков А, В и С и проведите через них плоскость ( Через любые три точки пространства, не лежащие на одной прямой, можно провести одну и только одну плоскость.)
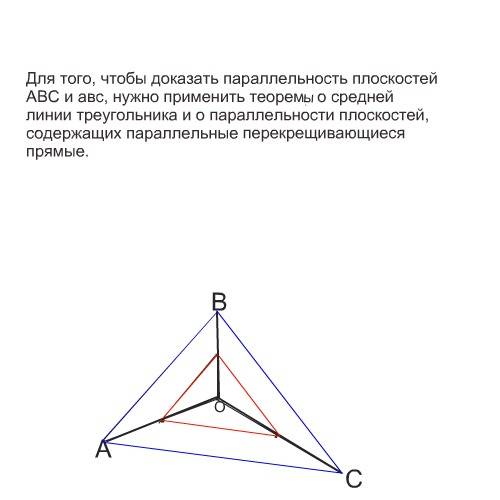
Обратите внимание на то, что при соединении свободных концов отрезков получились три треугольника:АОВ, ВОС и АОС.
Отрезки прямых, соединяющие середины сторон АО, ВО и ВС, соответственно параллельны сторонам АВ, ВС и АС как средние линии треугольников АОВ, ВОС и АОС. Проведенная через середины отрезков плоскость будет параллельна плоскости АВС :Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Что и требовалось доказать.
пусть середина АС обозначена за Е.
тр-к АОЕ имеет площадь 1/6 от площади треугольника АВС. Это прямоугольный треугольник с заданной гипотенузой АО = 13 и неизвестными углами.
Если обозначить угол ОАЕ (он же ОАС) за Ф, то
Sabc = 6*Saoe = 6*(1/2)*OE*AE = 3*AO^2*sin(Ф)*cos(Ф) = (3/2)*АО^2*sin(2Ф).
Ну, отсюда следует, что 0 < Ф < некий максимально возможный угол. Интересно, какой?
Примечание.
Есть формула для площади треугольника через его медианы, для равнобедренного треугольника она выглядит так.
S = (M/3)*корень((2*m)^2 - M^2); если опубликуют такую задачу - напишу решение.
В условиях задачи 2*m = 3*АО = 39. М - медиана к основанию, не задана. Видно, что максимальное значение M = 2*m, больше нельзя. Это соответствует странному случаю, когда АО перпендикулярно АС :)) Видимо, максимальный угол Ф все таки равен 90 градусов (это не доказательство, а просто замечание).
Вывод - условие неполное, необходимо еще что-то - чтобы узнать угол или какую-то длину. Фактически нам предложено однозначно определить треугольник по одной медиане, что некорректно. Бывает, что неполного условия достаточно, но тут не тот случай.
Рисунок чертить не буду, сам нарисуешь.
Докажем, что треугольники ВОС и АОД подобны. Углы ВОС и АОД равны, также углы ВСО и САД равны (накрестлежащие при пересечении прямой двух параллельных прямых). Значит треугольники ВОС и АОД подобны (по двум углам). Значит отношение все сторон равны.
Пусть AO - х, тогда ОС = 30-х. получаем
Тогда ОС = 30-18 = 12