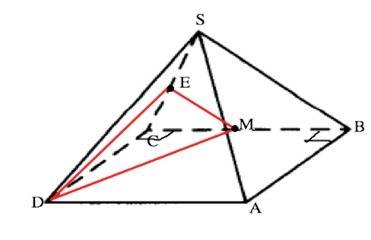
Прямые DE и SB не пересекаются, не параллельны и не лежат в одной плоскости. Они скрещивающиеся.
Чтобы найти угол между скрещивающимися прямыми, нужно:
Провести прямую, параллельную одной из двух скрещивающихся прямых так, чтобы она пересекала вторую прямую. При этом получатся пересекающиеся прямые. Угол между ними равен углу между исходными скрещивающимися.
CE=SE по условию; ЕМ ║ SB и является средней линией ∆ SCB.
Искомый угол – ∠DEM.
Так как все ребра пирамиды равны, её боковые грани - правильные треугольники. Примем длину ребер равной 1.
Тогда ЕМ=CM=1/2.
DE=DC•sin60°=√3/2
Из прямоугольного ∆DEM по т.Пифагора найдём DM²
DM²=CM²+DC²=(1/2)²+(√3/2)²=5/4
По т.косинусов
DM²=EM²+DE²-2•EM•DE•cos(DEM)
cosDEM=(DM²-(DE²+EM²)²(-2•DE•EM)
cosDEM=[5/4 - {1/2)²+(√3/2)²}:(-2•(1/2)•√3/2)= - (1/4) •2/√3=-1/2√3
Умножив числитель и знаменатель этой дроби на √3, получим:
ответ arccos=-√3/6
cos∠DEM= -0.2886751345948128812 По калькулятору это ≈ 106°47’43’’
1) Треуголник BOC равнобедренный значит угол OBC = OCB= (180-160)/2=10 градусов
2)треугольник BOA равнобедр следует угол OBA =углу OAB= (180-70)/2= 55градусов
3)угол AOC=360-30-160=170 градусов
4) Из треуг AOC угол OAC=углуOCA=(180-170)/2=5
5)Следует угол B=65 градусов, уго С= 15 градусов
6) Угол А равен 180-80 =100 градусов
ответ : 100 , 15, 65