Question

"расстояние от середины отрезка ab, пересекающего плоскость альфа, до плоскости альфа равно 15 см, а расстояние от точки a до плоскости альфа равно 12см. н айдите расстояние от точки b до плоскости альфа. " решить . a) 38 см; б) 32 см; в) 42 см; г) другой ответ.

Answer 1

Сделаем рисунок. Пусть С - середина отрезка АВ, О- точка его пересечения с плоскостью, АА1, СМ, ВК - перпендикуляры от точек прямой к плоскости и являются расстоянием до нее. 
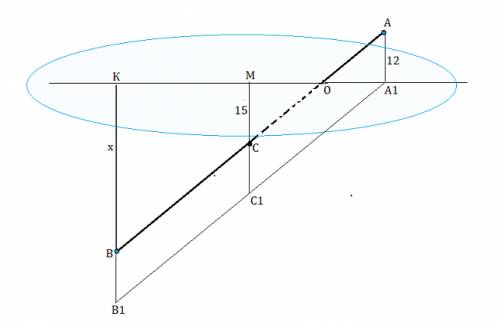
АА1=12 см.
СМ=15 см
ВК=х см
Проведем параллельно прямой АВ прямую А1В1.
АА1 || МС1 || КВ1 по построению
ВАА1В1- параллелограмм 
 В треугольнике А1КВ1 отрезок МС1- средняя линия и равен сумме 
МС+АА1=15+12 =27 см
КВ1=2 МС1=54 см
КВ1=ВК+12 ⇒
ВК=54-12=42 см

Answer 2

Обозначим на отрезок АВ как 2Х,тогда половина этого отрезка будет равна Х.
Обозначив точку К как точку пересечения отрезка АВ с плоскостью,а точку О как середину отрезка АВ,произведём сложения.
Сложив расстояния от АК+КО получим величину АО-половины отрезка,равное Х=15+12=27⇒
Тогда расстояние от точки В до плоскости будет ВК=ВО+ОК=27+15=42;
ответ  :расстояние от точки B до плоскости альфа будет равно 42;