Угол D = 120 градусов.
Объяснение:
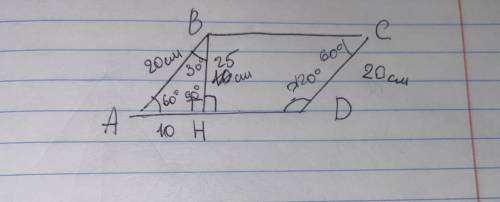
1. АВСД - параллелограмм, следовательно:
Ав=сд=20 см , угол а = углу с
2. Вн - высота, следовательно:
Угол ВНА = 90
3. Угол ВНА = 90 градусов, следовательно:
Треугольник ВНА - прямоугольный
4. Рассмотрим ВНА - прямоугольный треугольник:
СD=AB=20 см, АН=10 см
АВ - гипотенуза, АН -катет.
В прямоугольном треугольнике, если катет равен половине гипотенузы, то угол, лежащий против этого катета будет равен 30 градусам. Следовательно угол АВН = 30 градусам, тогда угол А = 180 - угол АВН - угол АНВ= 180 - 30 - 90 = 60
5. Угол А = углу С (по доказанному) = 60 градусам
6. Угол С + Угол Д = 180 градусов (односторонние углы при параллельных прямых в параллелограмме)
Тогда угол Д = 180 - угол С = 120 градусов
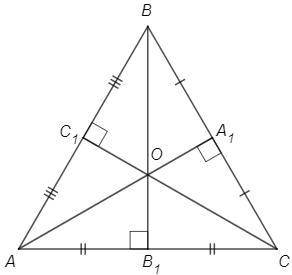
Медианы треугольника пересекаются в одной точке.
Высоты треугольника пересекаются в одной точке.
В данном треугольнике эти точки совпадают - медианы являются также высотами.
Совпадение медианы и высоты к основанию - признак равнобедренного треугольника.
Таким образом данный треугольник является равнобедренным относительно любой стороны, то есть равносторонним.
O - точка пересечения медиан, AA1 - медиана, A1 - середина BC.
O - точка пересечения высот (ортоцентр), AA1 проходит через точку O => AA1 - высота, AA1⊥BC
∠AA1B=∠AA1C=90 (AA1 - высота)
BA1=CA1 (AA1 - медиана)
△BAA1=△CAA1 (по двум катетам, AA1 - общий) => AB=AC
(Доказали: Если медиана треугольника совпадает с его высотой, то треугольник равнобедренный.)
Аналогично: BB1 - медиана и высота к стороне AC => AB=BC
AB=AC=BC, △ABC - равносторонний
0,9 см, если точка В находится между точками С и Д
точка Д находится между точками С и В по условиям данной задачи находится не может.