Угол между хордой и касательной равен половине градусной меры дуги, стягиваемой этой хордой (свойство), то есть половине градусной меры дуги АВ.
На дугу АВ опирается центральный угол АОБ, значит дуга АВ = 120°. Значит угол между касательной и хордой в точке касания равен 120°:2 = 60°
ответ: искомый угол равен 60°.
Или так:
В равнобедренном треугольнике АОВ (стороны ОА и ОВ равны - радиусы) углы при основании равны по (180-120):2=30° (сумма углов треугольника = 180°). Касательная в точке касания перпендикулярна радиусу, значит искомый угол равен 90° - 30° = 60°.
ответ: 60°
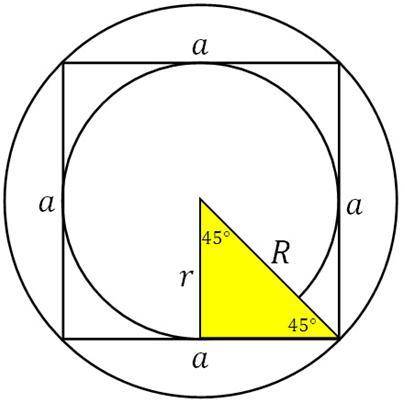
Задача: Радиус окружности, описанной около квадрата, равен 26√2. Найти радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, (R) равен полудиагонали этого квадрата, то есть вся диагональ (d) равна:
d = 2R = 2*26√2=52√2
Используя т. Пифагора, найдем длину стороны (a) квадрата:
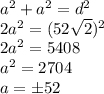
(отрицательное значение отбрасывает — не подходит по условию задачи)
Радиус окружности, вписанной в этот квадрат, (r) равен половине его стороны:
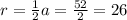
ответ: Радиус окружности, вписанной в квадрат, равен 26.
Так как BD- биссектриса=>угол ABD= углу DBС= угол ABC/2=78/2=39 градусов
ответ:90;39
2)так как D-середина AB=>BD=AD; так как Е-середина ВС=>СЕ=ВЕ; так как AD=EC=>BD=AD=CE=BE и AB=BC;
Треуголники АВЕ и СDB равны по двум сторонам и углу сежду ними(DB=BE; AB=BC; угол В- общий) Ч. Т. Д.
3)треугольники ОАВ и СОD равны по двум углам и ребру между ними ( OA=OC- по условию; угол А=углу С- по условию; угол О- общий) Ч. Т. Д.;
Так как треуголники равны=> у них все ребра тоже равны=> АВ=DC=15см
ответ: 15см